Ta có: OA = 5 cm, A'B' = 2AB. Tìm OF.
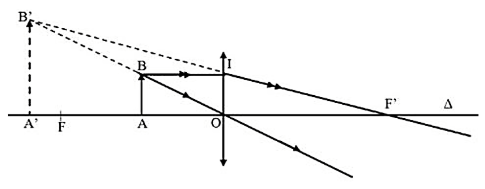
Do ∆ОАВ ~ ∆OA'B' và ∆FA'B' ~ ∆FOI
Nên\(\frac{{OA'}}{{OA}} = \frac{{A'B'}}{{AB}}\) \(\)(1) \(\frac{{OF}}{{OA' + OF}} = \frac{{OI}}{{A'B'}}\) (2) OI=AB (3)
Từ (1), (2) và (3) ta có:
\(\begin{array}{l}\frac{{OF}}{{OA' + \;OF}} = \frac{{OI}}{{A'B'}} = > \frac{{OF}}{{OA' + \;OF}} = \frac{{AB}}{{A'B'}} = > \frac{{OF}}{{OA' + \;OF}} = \frac{{OA}}{{OA'}}\\ = > OF.OA' = OA.OA' + OA.OF\\ = > OF(OA' - OA) = OA.OA'\\ = > \frac{1}{{\;OF}} = \frac{{OA' - OA}}{{OA'.OA}} = > \frac{1}{{\;OA}} - \frac{1}{{\;OA'}} = \frac{1}{{OF}}\end{array}\)
Mà \(\frac{{OA'}}{{OA}} = \frac{{A'B'}}{{AB}} = 2 = > OA' = 2OA = 2.5 = 10cm\)
Thay số vào ta được: \(\frac{1}{{\;OA}} - \frac{1}{{\;OA'}} = \frac{1}{{OF}} = > \frac{1}{{\;5}} - \frac{1}{{\;10}} = \frac{1}{{OF}} = > OF = 10cm\)



