Chiếu tia sáng từ không khí vào rượu với góc tới bằng 60o. Biết chiết suất của rượu là 1,36. Tính góc khúc xạ trong trường hợp này.
Bài tập (Chủ đề 2)
Câu hỏi 1 (SGK Khoa học tự nhiên 9 - Bộ sách Cánh diều - Trang 39)
Thảo luận (1)
Câu hỏi 2 (SGK Khoa học tự nhiên 9 - Bộ sách Cánh diều - Trang 39)
Ở hình 3.3, nếu thay tia sáng đỏ bằng ánh sáng trắng thì có xảy ra hiện tượng tán sắc ánh sáng không? Vẽ hình giải thích dự đoán của em.

Thảo luận (1)Hướng dẫn giảiKhi ánh sáng trắng chiếu vào khối thủy tinh, có thể xảy ra được hiện tượng tán sắc ánh sáng. Khi ánh sáng trắng chuyển từ không khí sang thủy tinh, ánh sáng bị phân tách và tạo ra dải màu sắc, giống như một cầu vồng.
Tuy nhiên, đối với thủy tinh, hiện tượng tán sắc này thường không rõ ràng bằng như với các vật liệu khác như viên pha lê hay các chất có cấu trúc tinh thể đặc biệt. Điều này là do cấu trúc của thủy tinh nên hiệu ứng tán sắc không được thể hiện rõ như trong một số vật liệu khác.
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi 3 (SGK Khoa học tự nhiên 9 - Bộ sách Cánh diều - Trang 39)
Trả lời câu hỏi bài 3 trang 39 SGK KHTN 9 Cánh diều
Ở hình 1, vì sao bông hoa hồng có màu đỏ và lá có màu xanh?

Thảo luận (1)Hướng dẫn giảiDưới ánh nắng mặt trời, ta nhìn thấy bông hoa hông có màu đỏ vì cánh hoa hồng đã hấp thụ các màu khác và cho phản xạ ánh sáng màu đỏ tới mắt. Tương tự, ta nhìn thấy lá của bông hồng có màu xanh vì lá của hoa hồng đã hấp thụ các màu khác và cho phản xạ ánh sáng màu xanh tới mắt.
(Trả lời bởi Nguyễn Quốc Đạt)
Câu hỏi 4 (SGK Khoa học tự nhiên 9 - Bộ sách Cánh diều - Trang 39)
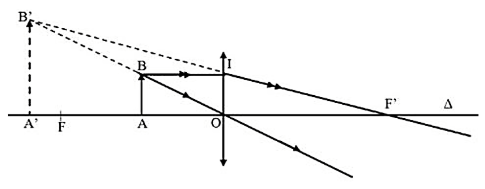
Dòng chữ trên trang sách được đặt cách thấu kính hội tụ 5 cm cho ảnh ảo có chiều cao gấp đôi. Tìm tiêu cự của thấu kính.
Thảo luận (1)Hướng dẫn giảiTa có: OA = 5 cm, A'B' = 2AB. Tìm OF.
Do ∆ОАВ ~ ∆OA'B' và ∆FA'B' ~ ∆FOI
Nên\(\frac{{OA'}}{{OA}} = \frac{{A'B'}}{{AB}}\) \(\)(1) \(\frac{{OF}}{{OA' + OF}} = \frac{{OI}}{{A'B'}}\) (2) OI=AB (3)
Từ (1), (2) và (3) ta có:
\(\begin{array}{l}\frac{{OF}}{{OA' + \;OF}} = \frac{{OI}}{{A'B'}} = > \frac{{OF}}{{OA' + \;OF}} = \frac{{AB}}{{A'B'}} = > \frac{{OF}}{{OA' + \;OF}} = \frac{{OA}}{{OA'}}\\ = > OF.OA' = OA.OA' + OA.OF\\ = > OF(OA' - OA) = OA.OA'\\ = > \frac{1}{{\;OF}} = \frac{{OA' - OA}}{{OA'.OA}} = > \frac{1}{{\;OA}} - \frac{1}{{\;OA'}} = \frac{1}{{OF}}\end{array}\)
Mà \(\frac{{OA'}}{{OA}} = \frac{{A'B'}}{{AB}} = 2 = > OA' = 2OA = 2.5 = 10cm\)
Thay số vào ta được: \(\frac{1}{{\;OA}} - \frac{1}{{\;OA'}} = \frac{1}{{OF}} = > \frac{1}{{\;5}} - \frac{1}{{\;10}} = \frac{1}{{OF}} = > OF = 10cm\)
(Trả lời bởi Nguyễn Quốc Đạt)