Trong Hình 4b, góc lượng giác là (Oz,Ot) với tia đầu là tia Oz và tia cuối là tia Ot
Bài 1. Góc lượng giác. Giá trị lượng giác của góc lượng giác
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{4\pi }}{3}\). Cho góc lượng giác \((O'u',O'v')\) có tia đầu \(O'u' \equiv Ou\), tia cuối \(O'v' \equiv Ov\). Viết công thức biểu thị số đo góc lượng giác \((O'u',O'v')\)
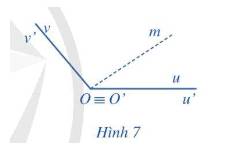
Trong Hình 7, hai góc lượng giác (Ou, Ov), \((O'u',O'v')\)có tia đầu trùng nhau \(Ou \equiv O'u'\), tia cuối trùng nhau \(Ov \equiv O'v'\). Nêu dự đoán về mối liên hệ giữa số đo của hai góc lượng giác trên.
Hãy biểu diễn trên mặt phẳng góc lượng giác gốc O có tia đầu Ou, tia cuối Ov và có số đo \( - \frac{{5\pi }}{4}\)
Cho góc lượng giác (Ou,Ov) có số đo là \( - \frac{{11\pi }}{4}\), góc lượng giác (Ou,Ow) có số đó là \(\frac{{3\pi }}{4}\). Tìm số đo của góc lượng giác (Ov,Ow).
Tìm giác trị lượng giác của góc lượng giác \(\beta = - \frac{\pi }{4}\)
Tìm các giá trị lượng giác của góc lượng giác \(\alpha = 45^\circ \)
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = - 30^\circ \)
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\)
Cho góc (hình học) xOz, tia Oy nằm trong góc xOz (Hình 8). Nêu mối liên hệ giữa số đo góc xOz và tổng số đo của hau góc xOy và yOz.




