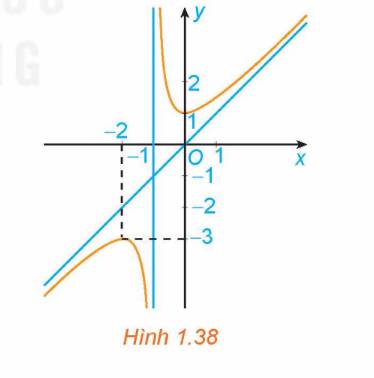
Đồ thị hàm số trong hình 1.38 có dạng: \(y = \frac{{a{x^2} + bx + c}}{{px + q}}\left( {a \ne 0,p \ne 0} \right)\) và đa thức tử không chia hết cho đa thức mẫu. Do đó, loại đáp án B.
Đồ thị hàm số trong hình 1.38 đi qua điểm \[\left( { - 2; - 3} \right)\]. Do đó, loại đáp án C.
Đồ thị hàm số trong hình 1.38 đi qua điểm (0; 1). Do đó, loại đáp án A.
Hàm số \(y = \frac{{{x^2} + x + 1}}{{x + 1}} = x + \frac{1}{{x + 1}}\) có:
+ \(\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{{x^2} + x + 1}}{{x + 1}} = + \infty ;\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{{x^2} + x + 1}}{{x + 1}} = - \infty \) nên đường thẳng \(x = - 1\) là tiệm cận đứng của đồ thị hàm số.
+ \(\mathop {\lim }\limits_{x \to + \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x + 1}} = 0\), \(\mathop {\lim }\limits_{x \to - \infty } \left( {y - x} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {x + \frac{1}{{x + 1}} - x} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x + 1}} = 0\) nên đường thẳng \(y = x\) là tiệm cận xiên của đồ thị hàm số.
Chọn D.