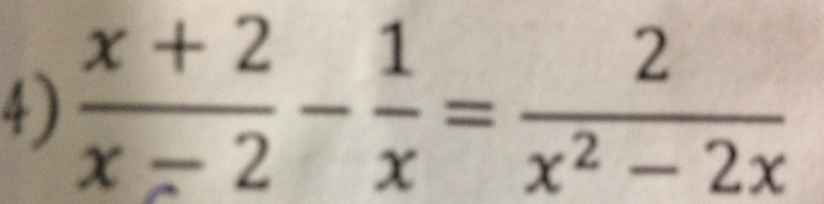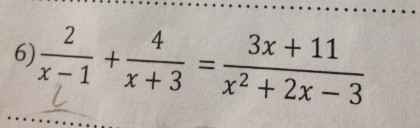\(ĐK:x\ne0;2\)
\(\Rightarrow\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+2\right)-\left(x-2\right)}{x\left(x-2\right)}=\dfrac{2}{x\left(x-2\right)}\)
\(\Leftrightarrow x\left(x+2\right)-\left(x-2\right)=2\)
\(\Leftrightarrow x^2+2x-x+2-2=0\)
\(\Leftrightarrow x^2+x=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
\(\dfrac{x+2}{x-2}-\dfrac{1}{x}=\dfrac{2}{x^2-2x}\) ĐKXĐ: x≠0, x≠2
<=>\(\dfrac{x\left(x+2\right)}{x\left(x-2\right)}-\dfrac{x-2}{x\left(x-2\right)}=\dfrac{2}{x\left(x-2\right)}\)
=>x(x+2) - x + 2 =2
<=>x\(^2\) + 2x - x = 2-2
<=> x\(^2\) + x =0
<=> x(x + 1) = 0
<=>\(\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
mà ĐKXĐ: x≠0, x≠2
Vậy x = -1