Question

Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và \(\widehat{AOB}=\alpha\left(0< \alpha< \dfrac{\pi}{4}\right)\). Gọi β là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox (H.4.31).a) Tính thể tích V của β theo a và α.b) Tìm α sao cho thể tích V lớn nhất.

Answer 1

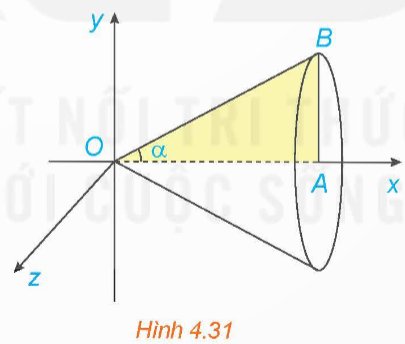
a) Ta có: \(AB = a\tan \alpha \). Khi quay tam giác AOB quanh trục Ox ta được khối nón tròn xoay có bán kính đáy \(r = AB = a\tan \alpha \) và chiều cao \(h = OA = a\).

Thể tích khối nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .a.{a^2}{\tan ^2}\alpha  = \frac{1}{3}\pi .{a^3}{\tan ^2}\alpha \) .

b) Theo a ta có: \(V = \frac{1}{3}\pi {a^3}{\tan ^2}\alpha \).

Ta có: \(V' = \frac{2}{3}\pi {a^3}\tan \alpha .\frac{1}{{{{\cos }^2}\alpha }}\). Với \(0 < \alpha  \le \frac{\pi }{4} \Rightarrow 0 < \tan \alpha  < 1\). Do đó, \(V' > 0\) nên hàm số V đồng biến trên \(\left( {0;\frac{\pi }{4}} \right)\).

Do đó, \(\mathop {\max }\limits_{\left( {0;\frac{\pi }{4}} \right]} V = V\left( {\frac{\pi }{4}} \right) = \frac{1}{3}\pi {a^3}{\tan ^2}\frac{\pi }{4} = \frac{1}{3}\pi {a^3}\).

Vậy giá trị lớn nhất của V là \(\frac{1}{3}\pi {a^3}\) khi \(\alpha  = \frac{\pi }{4}\).