Bài 6: Tam giác cân
Các câu hỏi tương tự
cho tam giác DEF có DI =12cmvuông góc EF tại I .Biết DF=20cm;DI=12cm;EI=9cm
a)tính độ dài IF,ED và chu vi của tam giác DEF
B)CM: tam giác DEF là tam giác vuông
cho tam giác cân DEF (DE=DF).Gọi N và M lần lượt là trung điểm của DE và DF,kẻ DH vuông góc với EF tại H
a) CM HE=HF
b) giả sử DE=DF=5cm,EF=8cm.Tính độ dài đoạn DH
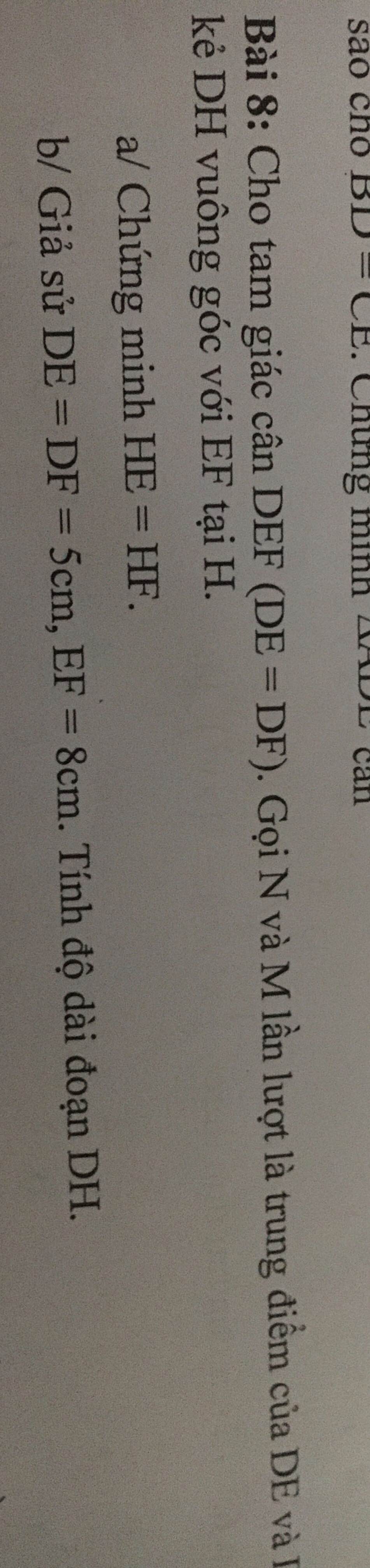
cho tam giác DEF cân tại D. Gọi H là trung điểm của EF
a)c/m:tam giác DEH=tam giác DFH và DH vuông góc EF
b) kẻ HM vuông góc DE tại M, HN vuông góc DF tại N. C/m tam giác HMNcân tại H
cho tam giác DEF cân tại D,gọi M là trung điểm EF a) chứng minh tam giác DEM tam giác DFM , từ đó chứng minh DM vuông góc EF b)trên tia đối tia ED lấy điểm K,tia đối của tia FD lấy điểm H sao cho EKFH.chứng minh tam giác DHK là tam giác cân c) chứng minh EF // HKd) gọi I là trung điểm HK .chứng minh D,M,I thẳng hàng e) chứng minh tam giác HFI tam giác KEI , từ đó chứng minh tam giác IEF là tam giác cân f) gọi M là trung điểm EK trên tia đối tia MI lấy điểm N sao cho MIMN ,chứng minh E,F...
Đọc tiếp
cho tam giác DEF cân tại D,gọi M là trung điểm EF
a) chứng minh tam giác DEM = tam giác DFM , từ đó chứng minh DM vuông góc EF
b)trên tia đối tia ED lấy điểm K,tia đối của tia FD lấy điểm H sao cho EK=FH.chứng minh tam giác DHK là tam giác cân
c) chứng minh EF // HK
d) gọi I là trung điểm HK .chứng minh D,M,I thẳng hàng
e) chứng minh tam giác HFI = tam giác KEI , từ đó chứng minh tam giác IEF là tam giác cân
f) gọi M là trung điểm EK trên tia đối tia MI lấy điểm N sao cho MI=MN ,chứng minh E,F,N thẳng hàng
Cho tam giác DEF có DE = DF. Tia phân giác của góc D cắt EF tại M.
a) Chứng minh: ∆DEM = ∆DFM.
b) Chứng minh DM vuông góc với EF
c) Chứng minh M là trung điểm của cạnh EF.
cho tam giác abc=tam giác def có ab=3cm,df=4cm,ef=5cm.tính chu vi của mỗi tam giác
Cho tam giác ABC cân tại A ; kẻ AD vuông góc BC ; DE vuông góc AB ; DF vuông góc AC: a) C/m tam giác ADB = tam giác ADC và DB = DC b) C/m AEF cân c) C/m EF// BC d) gọi I là trung điểm của EF, C/m A, I, D thẳng hàng
Cho tam giác ABC cân tại A ; kẻ AD vuông góc BC ; DE vuông góc AB ; DF vuông góc AC: a) C/m tam giác ADB = tam giác ADC và DB = DC b) C/m AEF cân c) C/m EF// BC d) gọi I là trung điểm của EF, C/m A, I, D thẳng hà...
Cho tam giác ABC đều,lấy điểm D trên cạnh BC sao cho BC=3BD,vẽ DE vuông góc với BC(E thuộc AB),vẽ DF vuông góc với AC(F thuộc AC).Chứng minh rằng tam giác DEF là tam giác đều









