Vì \(MN//EF\) nên theo định lý Thales, ta có: \(\frac{MD}{ME}=\frac{ND}{NF}\Leftrightarrow\frac{2}{2}=\frac{3,5}{NF}\)
\(\Rightarrow NF=3,5\left(cm\right)\)
KL: ................
Vì \(MN//EF\) nên theo định lý Thales, ta có: \(\frac{MD}{ME}=\frac{ND}{NF}\Leftrightarrow\frac{2}{2}=\frac{3,5}{NF}\)
\(\Rightarrow NF=3,5\left(cm\right)\)
KL: ................
( Sử dụng định lý Talet) Cho ∆DEF nhọn , DE<DF. Lấy M thuộc DE, N thuộc DF sao
cho MN// EF. Cho biết DE= 6cm, ME= 2cm
a) Tính độ dài MD
b) Tính tỉ số MD/ME và MD/DE
c) Tính tỉ số DN/NF và DN/DF
(Sử dụng định lý Talet) Cho ∆DEF nhọn , DE<DF. Lấy M thuộc DE, N thuộc DF sao
cho MN// EF. Cho biết DE= 6cm, ME= 2cm
a) Tính độ dài MD
b) Tính tỉ số \(\frac{MD}{ME}\) và \(\frac{MD}{DE}\)
c) Tính tỉ số \(\frac{DN}{NF}\) và \(\frac{DN}{DF}\)
Gi úp em với
cho tam giác DEF có DE =9cm , DF = 15 cm , EF = 21 cm . lấy M,N, thuộc DE , DF sao cho DM = 3cm , DN = 5cm
a, chứng minh MN //EF
b, Tính MN
c, kẻ trung tuyến DI của tam giác DEF . DI cắt MN tại K . Chứng minh K là trung điểm MN
cho tam giác DEF vuông tại D có DE=9cm,DF=12cm,lấy điểm H thuộc cạnh DF sao cho góc DEH=góc DFE.
a) chứng minh tam giác DEF đồng dạng với tam giác DHE
b) chứng minh DE2=DH . DF
c) tính diện tích tam giác DHE
d) phân giác góc D cắt cạnh EF tại G, cắt cạnh EH tại I. chứng minh IE . EG =IH . GF
Cho tam giác ABC có độ dài cạnh BC=a=15 cm . Trên cạnh lấy ba điểm D,E,F sao cho AD=DE=EF=FB. Trên cạnh AC lấy ba điểm M,N,P sao cho AM=MN=NP=PC . Tính độ dài các đoạn thẳng DM,EN,FP
( Sử dụng hệ quả của định lý Talet) Cho ∆ABC nhọn , AB<AC. Vẽ đường thẳng song
song với cạnh BC cắt cạnh AB ở D và cắt cạnh AC tại E. Cho biết AD = 2cm, AB = 5cm, BC
= 10cm
a) Tính AD/AB
b) Tính DE/BC
c) Tính DE
Cho tam giác ABC, từ điểm D trên cạnh AB kẻ đường thẳng song song với BC cắt AC tại E. Tính các cạnh AE, DE của tam giác ADE biết AB=6cm, AD=2cm, AC=4,8cm, BC=5,1cm
Bài 6: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Kẻ IM song song với BK, M thuộc AC, kẻ KN song song với CI, N thuộc AB.
a) Chứng minh MN song song với BC.
b) Gọi E là trung điểm của BC, F là giao điểm của BK và AE, H là giao điểm của CF và AB. Chứng minh HK song song với BC.
Cho tam giác ABC có cạnh BC = a. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M, N (h.5).
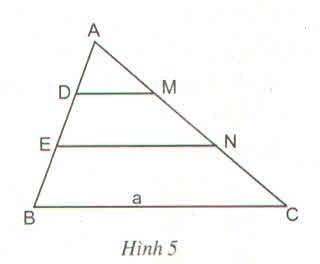
Tính theo a độ dài của các đoạn thẳng DM và EN ?