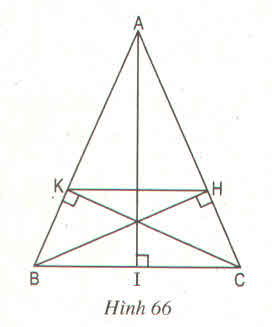
Chỉ biết làm 2 câu đầu tiên thôi :((( xin lỗi nha
a) Xét tam giác KCB và tam giác HBC có:
BC chung
\(\widehat{KBC}=\widehat{HBC}\left(gt\right)\)
\(\widehat{H}=\widehat{K}\left(=90^0\right)\)
\(\Rightarrow\Delta KCB=\Delta HCB\)
\(\Rightarrow BK=CH\)
b) Ta có: AB = AC ( tam giác cân ABC )
BK = CH ( câu a )
\(\Rightarrow\dfrac{BK}{AB}=\dfrac{HC}{AC}\)
Suy ra KH // BC ( định lý Ta-lét đảo )
Xét \(\Delta BKC\) và \(\Delta CHB\), Có:
\(\left\{{}\begin{matrix}\widehat{B}=\widehat{H}\left(gt\right)\\BC.chung\\\widehat{K}=\widehat{H}\left(=90^o\right)\end{matrix}\right.\)
\(\Rightarrow\) \(\Delta BKC\) = \(\Delta CHB\) (g.c.g)
\(\Rightarrow BK=CH\) (2 cạnh tương ứng)
b) Ta có:
\(\left\{{}\begin{matrix}AC=AB\\BK=HC\end{matrix}\right.\Rightarrow\dfrac{BK}{AB}=\dfrac{HC}{AC}\)
\(\Rightarrow KH\) // BC (định lý ta lét đảo)

a, Xét \(\Delta\)HBC và \(\Delta\)KCB, ta có:
\(\widehat{HCB}=\widehat{KBC}\) (\(\Delta\)ABC cân tại A)
BC chung
\(\widehat{HBC}=\widehat{KCB}\) (\(=90^0-\widehat{HCB}=90^0-\widehat{KBC}\))
\(\Rightarrow\) \(\Delta\)HBC = \(\Delta\)KCB (g.c.g) \(\Rightarrow\) BK = CH
b, Xét \(\Delta\)ABC và \(\Delta\)AKH có:
\(\widehat{A}\) chung
\(\dfrac{AB}{AK}=\dfrac{AC}{AH}\) (AB=AC và AK=AH)
\(\Rightarrow\) \(\Delta\)ABC \(\sim\) \(\Delta\)AKH
\(\widehat{ABC}=\widehat{AKH}\)
KH // BC (đồng vị)
c, Theo c/m phần b, ta có:
\(\Delta\)ABC \(\sim\) \(\Delta\)AKH \(\Rightarrow\) \(\dfrac{AC}{BC}=\dfrac{AH}{HK}\) \(\Rightarrow\) \(\dfrac{a}{b}=\dfrac{AH}{HK}\) \(\Rightarrow\) HK = \(\dfrac{AH\cdot a}{b}\); AH = \(\dfrac{HK\cdot a}{b}\) \(\Rightarrow\) HC = AB - AH = a - \(\dfrac{HK\cdot a}{b}\) = \(\dfrac{ab-HK\cdot a}{b}\)