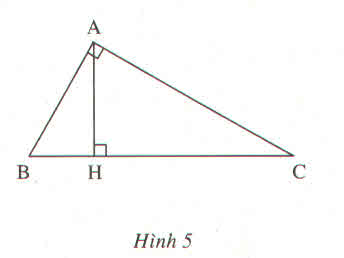
Ta có \(\dfrac{AB}{AC}=\dfrac{5}{4}\Rightarrow AC=\dfrac{4}{5}.AB\Rightarrow AC^2=\dfrac{16}{25}AB^2\)
Ta lại có △ABC vuông tại A⇒ BC2=AB2+AC2⇒225=\(AB^2+\dfrac{16}{25}AB^2=\dfrac{41}{25}AB^2\Rightarrow AB^2=225\div\dfrac{41}{25}=\dfrac{5625}{41}\Rightarrow AB=\dfrac{75\sqrt{41}}{41}\left(cm\right)\Rightarrow AC=\dfrac{4}{5}.AB=\dfrac{4}{5}.\dfrac{75\sqrt{41}}{41}=\dfrac{60\sqrt{41}}{41}\left(cm\right)\)Ta có △ABC vuông tại A đường cao AH⇒\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{\dfrac{5625}{41}}+\dfrac{1}{\dfrac{3600}{41}}=\dfrac{1681}{90000}\Rightarrow AH^2=\dfrac{90000}{1681}\Rightarrow AH=\dfrac{300}{41}\left(cm\right)\)Ta có △ABC vuông tại A đường cao AH⇒BC2=BH.BC⇒\(BH=\dfrac{AB^2}{BC}=\dfrac{\dfrac{5625}{41}}{15}=\dfrac{375}{41}\left(cm\right)\)
Ta có BC=BH+CH⇒CH=BC-BH=\(15-\dfrac{375}{41}=\dfrac{240}{41}\left(cm\right)\)