Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Gọi M là trung điểm của BC. Điểm D đối xứng với A qua M.
a) Chứng minh tứ giác ABDC là hình chữ nhật. Tính SABDC.
b) Kẻ AH vuông góc với BC ( H thuộc BC ). Gọi E là điểm đối xứng với A qua H. Chứng minh HM // DE
c) Tính tỉ số SAHM / SAED
d) Chứng minh tứ giác BCDE là hình thang cân
Ta có hình vẽ:
a/ Ta có: BM = MC (M là trung điểm BC)
AM = MD (D đối xứng vs A qua M)
A = 900 (tam giác ABC vuông tại A)
=> ABDC là hình chữ nhật.
SABCD = AB.AC = 6.8 = 48 cm2.
b/ Ta có: M là trung điểm AD (D đối xứng A qua M)
và H là trung điểm AE (E đối xứng A qua M)
=> MH là đường trung bình của tam giác ADE
=> HM // DE (đpcm).
c/ HM là đường trung bình => HM = 1/2 DE.
Ta có: AM = 1/2 AD
Ta có: AH = 1/2 AE
=> SAHM / SAED = 1/2.





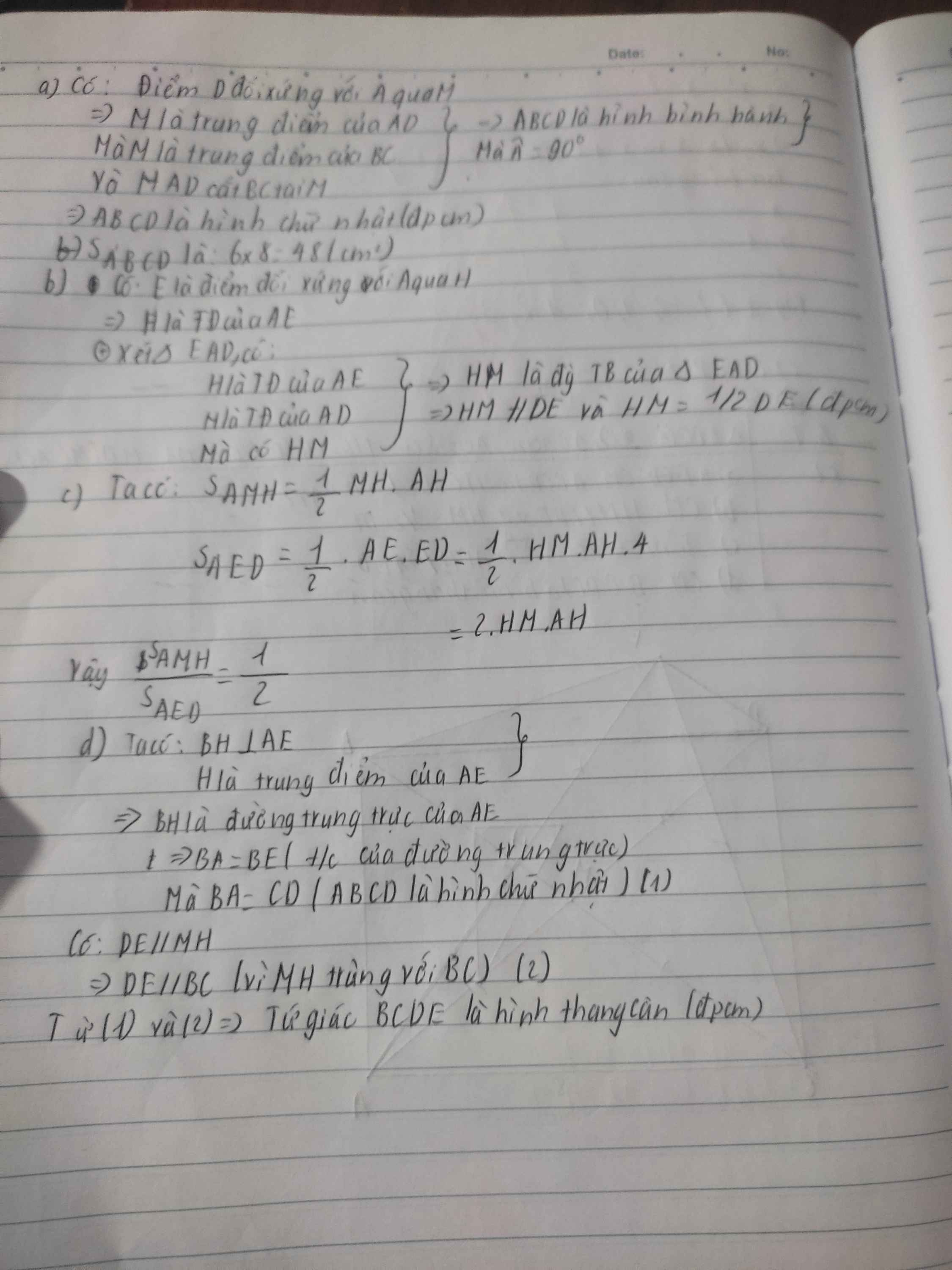 Đúng nhớ cho 1 like nha. Mình cảm ơn
Đúng nhớ cho 1 like nha. Mình cảm ơn 







