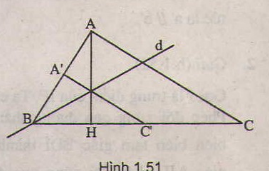
Gọi d là đường phân giác của . Ta có
biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp và Dd sẽ biến
HBA thành
ABC.
Gọi d là đường phân giác của . Ta có
biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp và Dd sẽ biến
HBA thành
ABC.
a) Gọi Bd là tia phân giác của \(\widehat{ABC}\).
Ta có: \(Đ_d\) biến tam giác AHB thành tam tam giác A'BH'.
Phép vị tự \(V_{\left(B;\dfrac{AH}{BC}\right)}\) biến tam giác A'BH thành tam giác CBA.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép \(Đ_d\) và \(V_{\left(B;\dfrac{AH}{BC}\right)}\) sẽ biến tam giác HBA thành tam giác ABC.