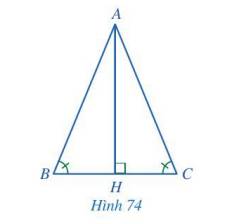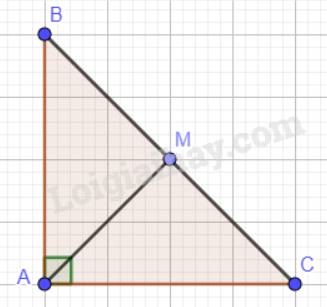
Tam giác ABC vuông cân tại A nên \(\widehat A = 90^\circ ;\widehat B = \widehat C; AB = AC\).
Tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat C = 90:2 = 45^\circ \).
Xét tam giác ABM và tam giác ACM có:
AB = AC
AM chung
BM = CM
\(\Rightarrow \Delta ABM = \Delta ACM\) (c.c.c)
\(\Rightarrow \widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng)
Mà \(\widehat {BAM} + \widehat {CAM}=\widehat{BAC}=90^0\)
\(\Rightarrow \widehat {BAM} = \widehat {CAM} = 90:2 = 45^\circ \).
Xét tam giác MAB: \(\widehat {MBA} = \widehat {BAM} = 45^\circ \Rightarrow \widehat {BMA} = 90^\circ ;MB = MA\).
Vậy tam giác MAB vuông cân tại M.