Question

Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp vào chỗ chấm hỏi để được các đẳng thức:

BG = ? BN, CG = ? CP;

BG = ? GN, CG = ? GP.

Answer 1

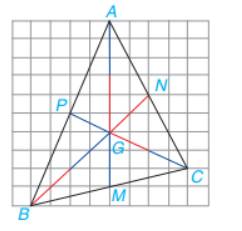
Vì G là trọng tâm của \(\Delta ABC\) nên \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\)

Ta có: \(GN = BN – BG = BN - \dfrac{2}{3}BN = \dfrac{1}{3}BN;\\ GP = CP – CG = CP - \dfrac{2}{3}CP = \dfrac{1}{3}CP\)

Do đó, \(BN = 3. GN ; CP = 3. GP\)

Như vậy, \(BG = \dfrac{2}{3}BN = \dfrac{2}{3}.3.GN = 2GN;\\CG = \dfrac{2}{3}CP = \dfrac{2}{3}.3.GP = 2GP\)

Vậy \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\);

\(BG = 2GN; CG = 2GP\).