c.
Theo giả thiết E và F cùng nhìn AH dưới 1 góc vuông
\(\Rightarrow AEHF\) nội tiếp
\(\Rightarrow\widehat{HEF}=\widehat{HAF}\) (cùng chắn HF)
E và D cùng nhìn AB dưới 1 góc vuông
\(\Rightarrow ABDE\) nội tiếp
\(\Rightarrow\widehat{BED}=\widehat{BAD}\) (cùng chắn BD) hay \(\widehat{BED}=\widehat{HAF}\)
\(\Rightarrow\widehat{HEF}=\widehat{BED}\)
\(\Rightarrow EH\) là phân giác của \(\widehat{DEF}\)
Chứng minh hoàn toàn tương tự ta có FH là phân giác của \(\widehat{DFE}\)
\(\Rightarrow H\) là giao điểm 2 đường phân giác trong của tam giác DEF
\(\Rightarrow H\) là tâm đường tròn nội tiếp tam giác DEF
d.
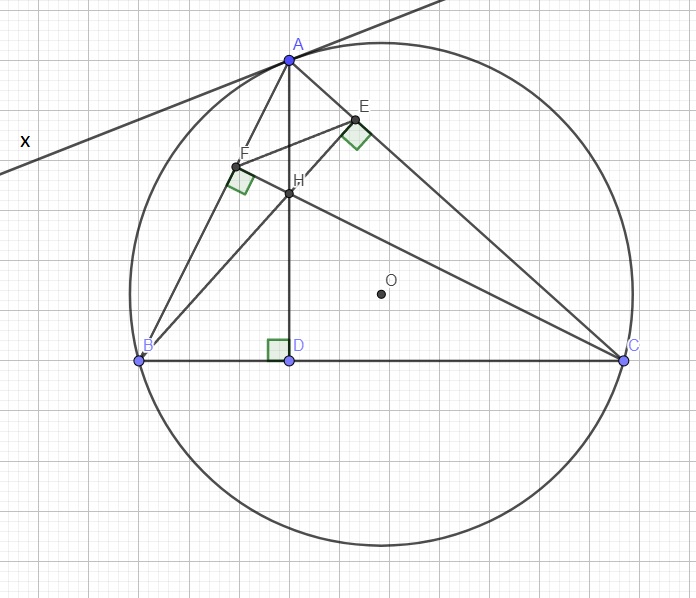
Trong đường tròn (O), qua A kẻ tiếp tuyến Ax
\(\Rightarrow Ax\perp OA\) (1)
Ta có: \(\widehat{BAx}=\widehat{BCA}\) (cùng chắn AB)
Mà \(\widehat{BCA}=\widehat{AFE}\) (theo cm câu b)
\(\Rightarrow\widehat{BAx}=\widehat{AFE}\)
\(\Rightarrow Ax||EF\) (hai góc so le trong bằng nhau) (2)
(1);(2) \(\Rightarrow OA\perp EF\)
a.
\(\left\{{}\begin{matrix}BE\perp CE\left(gt\right)\\BF\perp CF\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\) \(\widehat{BEC}=\widehat{BFC}=90^0\)
\(\Rightarrow\) Hai điểm E và F cùng nhìn BC dưới 1 góc vuông nên tứ giác BFEC nội tiếp
b.
Do BFEC nội tiếp \(\Rightarrow\widehat{BFE}+\widehat{BCA}=180^0\)
Mà \(\widehat{AFE}+\widehat{BFE}=180^0\) (hai góc kề bù)
\(\Rightarrow\widehat{AFE}=\widehat{BCA}\)
Xét hai tam giác ABC và AEF có:
\(\left\{{}\begin{matrix}\widehat{A}-chung\\\widehat{BCA}=\widehat{AFE}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABC\sim\Delta AEF\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AE}=\dfrac{AC}{AF}\Rightarrow AE.AC=AF.AB\)