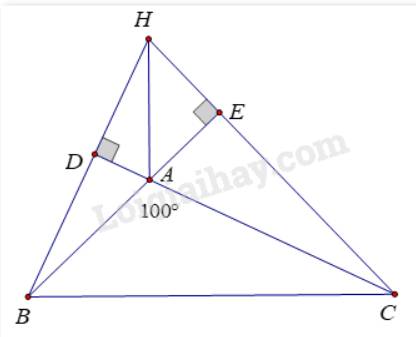
Gọi E là chân đường cao từ C xuống AB, D là chân đường cao từ B xuống AC
=> HC ⊥ BE, HB ⊥ CD
Ta có: Vì \(\widehat {BAC}\) và \(\widehat {BAD}\) là 2 góc kề bù nên
\(\begin{array}{l}\widehat {BAC} + \widehat {BAD} = {180^0}\\ \Rightarrow {100^0} + \widehat {BAD} = {180^0}\\ \Rightarrow \widehat {BAD} = {180^0} - {100^0}\\ \Rightarrow \widehat {BAD} = {80^0}\end{array}\)
∆ ADB là tam giác vuông tại D:
\(\begin{array}{l}\widehat {BAD} + \widehat {ABD} = {90^0}\\ \Rightarrow {80^0} + \widehat {ABD} = {90^0}\\ \Rightarrow \widehat {ABD} = {10^0}\end{array}\)
∆ BEH là tam giác vuông tại E
\(\begin{array}{l}\widehat {EBH} + \widehat {BHE} = {90^0}\\ \Rightarrow {10^0} + \widehat {BHE} = {90^0}\\ \Rightarrow \widehat {BHE} = {80^0}\end{array}\)
Hay \(\widehat {BHC} = {80^0}\)




