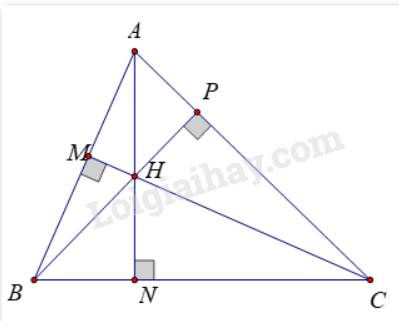
a)
Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M
Trong ΔAHB, ta có:
HM ⊥ AB
BN ⊥ AH
Mà MH cắt BN tại C
=> C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
HP ⊥ AC
CN ⊥ AH
Mà HP cắt CN tại B
=> B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
HN ⊥ BC
BM ⊥ HC
Mà HN cắt BM tại A
=> A là trực tâm của tam giác HBC.
Cho hai đường thẳng không vuông góc b,c cắt nhau tại điểm A và cho điểm H không thuộc b và c (H.9.47). Hãy tìm điểm B thuộc b, điểm C thuộc c sao cho tam giác ABC nhận H làm trực tâm.
Cho tam giác ABC có \(\widehat A = {100^0}\) và trực tâm H. Tìm góc BHC.
Sử dụng tính chất đường trung trực của một đoạn thẳng, hãy giải thích nếu điểm Q cách đều 3 đỉnh của tam giác ABC thì Q phải là giao điểm ba đường trung trực của tam giác ABC.
Vẽ tam giác ABC (không tù) và ba đường trung trực của các đoạn BC, CA, AB. Quan sát hình và cho biết ba đường trung trực đó có cùng đi qua một điểm hay không?
a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều 3 đỉnh của tam giác đó.
Xét điểm O cách đều 3 đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Mỗi tam giác có mấy đường trung trực?
Vẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không?
