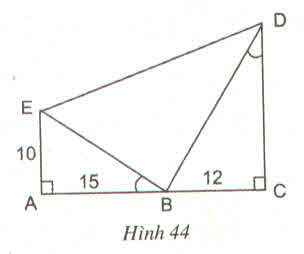
Lời giải:
Xét tam giác $BDC$ và $ABC$ có:
$\widehat{BDC}=\widehat{ABC}$ (gt)
$\widehat{C}$ chung
$\Rightarrow \triangle BDC\sim \triangle ABC$ (g.g)
$\Rightarrow \frac{BD}{AB}=\frac{DC}{BC}=\frac{BC}{AC}$
$\Rightarrow BC^2=AC.DC=(AD+DC).DC=(7+9).9=144$
$\Rightarrow BC=12$
$\Rightarrow \frac{BD}{AB}=\frac{DC}{BC}=\frac{9}{12}=\frac{3}{4}$
Cho ΔABC có AB = 14cm, AC = 28cm. Trên cạnh AC lấy điểm D sao cho: AD = 7cm. CMR: \(\widehat{ABD}\) = \(\widehat{ACB}\)
Cho hình thang ABCD có \(\widehat{A}=\widehat{D}=90^{\bigcirc}\), hai đường chéo AC và BD vuông góc với nhau. Biết AB=4cm, CD=9cm.
a) Chứng minh hai tam giác ADB ∼ DCA.
b) Tính độ dài AD.
c) Gọi M là giao điểm của AD và BC. Tính diện tích tam giác AMB
Hai tam giác ABC và DEF có \(\widehat{B}=\widehat{E}\), AB = 8cm, BC = 10cm, DE = 6cm. Tính độ dài các cạnh AC, DF và EF, biết rằng cạnh AC dài hơn cạnh DF là 3cm ?
Cho tam giác ABC trong đó AB = 15 cm, AC = 80 cm. Trên hai cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = 8cm, AE = 6cm. Hai tam giác ABC và ADE có đồng dạng với nhau không ? Vì sao ?
Hình 44 cho biết \(\widehat{EBA}=\widehat{BDC}\)
a) Trong hình vẽ có bao nhiêu tam giác vuông ? Hãy kể tên các tam giác đó
b) Cho biết AE = 10cm, AB = 15cm, BC = 12 cm. Hãy tính độ dài các đoạn thẳng CD, BEm BD và ED (làm tròn đến chữ số thập phân thứ nhất)
c) So sánh diện tích tam giác BDE với tổng diện tích của hai tam giác AEB và BCD
cho tam giác ABC vuông tại A có AB=6cm ,AC=8cm. đường cao AH và phân giác BDcắt nhau tại I (H trên BC và D trên AC)
a)tính độ dài AD,DC
b)Chướng minh tam giác ABC đồng dạng tam giác HBA và AB2=BH.BC
c)chứng minh tam giác ABI đồng dang với tam giác CBD
cho tam giác ABC cân tại A vẽ đường phân giác AD ( D thuộc BC ) A) chứng minh tam giác ADB đồng dạng tam giác ADC B) biết AB = 6cm BC= 8cm tính DB,DC
Cho \(\Delta\)ABC cân tại A, BC = 2a, M là trung điểm BC. Lấy D và E trên AB và AC sao cho \(\widehat{DME}=\widehat{B}\). CM :
a) \(\Delta BDM\sim\Delta CME\)
b) \(\Delta MDE\sim\Delta DBM\)
c) BD*CE ko đổi
Cho tam giác ABC có ba góc nhọn, AB=2cm, AC=4cm. Trên cạnh AC lấy điểm M sao cho góc ABM bằng góc ACB.
a) CMR: ΔABM∼ΔACB.
b) Từ A kẻ AH⊥BC, AK⊥BM. CMR:\(S_{AHB}=4S_{AKM}\)
