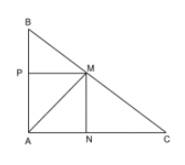
a) Ta thấy \(A{B^2} + A{C^2} = B{C^2}\)
=> Tam giác ABC vuông tại A
Có AC ⊥ AB
mà MP ⊥ AB
=> MP // AC
=> \(\widehat {BMP} = \widehat {MCN}\) (2 góc đồng vị)
Xét tam giác vuông BMP (vuông tại P) và tam giác MCN (vuông tại N) có \(\widehat {BMP} = \widehat {MCN}\)
=> ΔBMP ∽ ΔMCN
b) Xét tam giác BMP và tam giác BAC có MP // AC
=> \(\widehat {BMP} = \widehat {BAC}\)
=> \(\frac{4}{{40}} = \frac{{PM}}{8}\)
=> PM=3,2(cm)
=> BP=2,4 (áp dụng định lý Pythagore trong tam giác vuông BMP)
=> AP=3,6 (cm)
=> \(AM = \sqrt {23,2} \)(áp dụng định lý Pythagore trong tam giác vuông AMP)