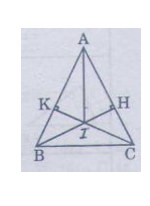
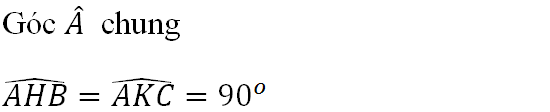Chứng minh :
Có △ABC cân tại A ⇒ AB = AC ( tính chất )
\(\Rightarrow\widehat{B}=\widehat{C}\left(\text{tính chất}\right)\)
Xét △BKC cân tại K và △CHB cân tại H có:
\(\widehat{B}=\widehat{C}\) ( cmt )
BC - cạnh chung
⇒ △BKC = △CHB ( cạnh huyền - góc nhọn )
⇒ BK = CH ( tương ứng )
Có K ∈ AB ⇒ K nằm giữa A và B
⇒ AK + KB = AB
⇒ AK = AB - KB \(\left(1\right)\)
Có H ∈ AC ⇒ H nằm giữa A và C
⇒ AH + HC = AC
⇒ AH = AC - HC \(\left(2\right)\)
mà AB = AC ( cmt ) ; KB = HC ( cmt )
Từ ( 1 ) và ( 2 ) ⇒ AK = AH
Xét △AKI vuông tại K và △AHI vuông tại H có :
AK = AH ( cmt )
AI - cạnh chung
⇒ △AKI = △AHI ( cạnh góc vuông - cạnh huyền)
\(\Rightarrow\widehat{KAI}=\widehat{HAI}\left(\text{tương ứng}\right)\)
⇒ AI là tia phân giác của \(\widehat{A}\)
Giải:
a) Xét ΔABH và ΔACK có:
AB = AC (gt)
Nên Δ ABH = Δ ACK (cạnh huyền – góc nhọn).
b) Hai tam giác vuông AIK và AIH có
AH = AK (gt)
AI chung
Vậy AI là tia phân giác của góc A.