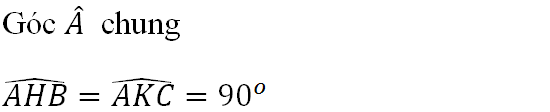a,
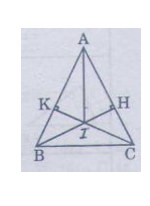
Xét ∆KCB và ∆HBC, ta có:
- BC chung [gt]
- \(\widehat{B}=\widehat{C}\) [∆ABC cân tại A]
=> ∆KCB = ∆HBC [ch-gn]
=> BK = CH
Mà AB = AC [∆ABC cân tại A]
=> AB - BK = AC - CH
=> AH = AK
b,
Xét ∆AKI và ∆AHI, ta có:
- AI chung [gt]
- AK = AH [câu a]
=> ∆AKI = ∆AHI [ch-cgv]
=> \(\widehat{IAK}=\widehat{IAH}\)
=> AI là tia p/g của góc A
Giải:
a) Xét ΔABH và ΔACK có:
AB = AC (gt)
Nên Δ ABH = Δ ACK (cạnh huyền – góc nhọn).
b) Hai tam giác vuông AIK và AIH có
AH = AK (gt)
AI chung
Vậy AI là tia phân giác của góc A.
Bạn áp dụng hình dưới nhé
a)Xét tam giác ABH và tam giác ACK ,có
AB=AC(gt)
Góc A chung
Suy ra:tam giác ABH =tam giác ACK (cạnh huyền_góc nhọn)
Suy ra:AH=AK
b)Xét tam giác AIK và tam giác AIH có,
AK=AH(chứng minh trên )
AI chung
Góc IAK = góc AIH
Suy ra:tam giác AIK = tam giác AIH(cạnh huyền_cạnh góc vuông)
Suy ra:AI là tia phân giác của góc A
Ko bt đúng không nữa nha :))
a) Xét tam giác AKC và tam giác AHB ,có :
AC = AB ( gt )
góc A : chung
góc AKC = góc AHB ( = 90o )
=> tam giác AKC = tam giác AHB ( ch - gn )
=> AK = AH ( hai cạnh tương ứng )
Vậy AK = AH
b) Xét tam giác AIB và tam giác AIC ,có :
AI : chung
AB = AC ( gt )
góc ABI = góc ACI ( tam giác AKC = tam giác AHB )
=> tam giác AIB = tam giác AIC ( c-g-c )
=> góc BAI = góc CAI ( hai góc tương ứng ) mà AI nằm giữa AB và AC => AI là tia phân giác của góc A
Vậy AI là tia phân giác của góc A
Xét \(\Delta ABH\perp H\) và \(\Delta ACK\perp K\) có :
AC = AB (gt)
\(\widehat{BAC}\) : góc chung
\(\Rightarrow\Delta ABH=\Delta ACK\left(c.h-g.n\right)\)
\(\Rightarrow\) AH = AK
Xét \(\Delta AKI\perp K\) và \(\Delta AHI\perp H\) có :
AK = AH (cmt)
AI : cạnh chung
\(\Rightarrow\Delta AKI=\Delta AHI\left(c.h-c.g.v\right)\)
\(\Rightarrow\widehat{KAI}=\widehat{HAI}\)
\(\Rightarrow\) AI là tia phân giác của \(\widehat{BAC}\)