Cho sơ đồ hình cây dưới đây
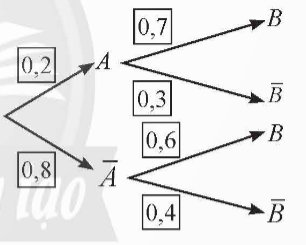
a) Xác suất của biến cố cả A và B đều không xảy ra là
A. 0,32. B. 0,4. C. 0,8. D. 0,92.
b) Xác suất của biến cố B là
A. 0,42. B. 0,62. C. 0,28. D. 0,48.
c) Xác suất điều kiện P(A|B) là
A. \(\dfrac{7}{31}\). B. \(0,7.\) C. \(\dfrac{7}{50}\). D. \(0,48\).
d) Giá trị của biểu thức \(\dfrac{P\left(B\right)P\left(\overline{A}\text{|}B\right)}{P\left(\overline{A}\right)}\) là
A. 0,48. B. 0,3. C. 0,5. D. 0,6.
a) Dựa vào sơ đồ hình cây, xác suất của biến cố cả \(A\) và \(B\) đều không xảy ra là
\(P\left( {\bar A\bar B} \right) = 0,8.0,4 = 0,32\).
Vậy đáp án đúng là A.
b) Với công thức xác suất toàn phần, ta có
\(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\bar A} \right).P\left( {B|\bar A} \right)\).
Dựa vào sơ đồ hình cây, ta có \(P\left( A \right) = 0,2\); \(P\left( {B|A} \right) = 0,7\); \(P\left( {\bar A} \right) = 0,8\); \(P\left( {B|\bar A} \right) = 0,6\).
Do đó \(P\left( B \right) = 0,2.0,7 + 0,8.0,6 = 0,62\).
Vậy đáp án đúng là B.
c) Sử dụng công thức Bayes, ta có \(P\left( {A|B} \right) = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( B \right)}}\).
Ta có \(P\left( A \right) = 0,2\); \(P\left( {B|A} \right) = 0,7\); \(P\left( B \right) = 0,62\).
Suy ra \(P\left( {A|B} \right) = \frac{{0,2.0,7}}{{0,62}} = \frac{7}{{31}}\).
Vậy đáp án đúng là A.
d) Ta có \(P\left( {A|B} \right) = \frac{7}{{31}}\), suy ra \(P\left( {\bar A|B} \right) = 1 - \frac{7}{{31}} = \frac{{24}}{{31}}\).
Ta có \(P\left( {\bar A} \right) = 0,8\). Như vậy \(\frac{{P\left( B \right)P\left( {\bar A|B} \right)}}{{P\left( {\bar A} \right)}} = \frac{{0,62.\frac{{24}}{{31}}}}{{0,8}} = 0,6\).
Vậy đáp án đúng là D.


