.png)
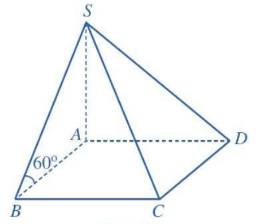
Gọi \(M\) là trung điểm của \(BC\), \(O\) là trọng tâm tam giác \(ABC\).
\( \Rightarrow SO \bot \left( {ABC} \right)\)
Tam giác \(ABC\) đều
\( \Rightarrow AM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
Tam giác \(SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SO = \frac{{{a^3}\sqrt 2 }}{{12}}\end{array}\)