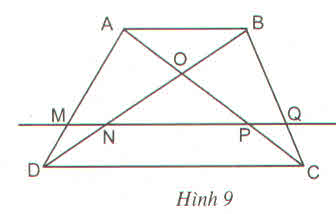
Để chứng minh rằng MN=PQ, ta sẽ sử dụng tính chất của các tam giác đồng dạng.
Gọi X là giao điểm của MQ và NP.
Ta có các tam giác đồng dạng sau:
MQX và NPX (do MQ song song với NP, XM song song với PN và góc MXQ và PXN là góc đồng phía nội tiếp giữa hai đoạn thẳng MQ và NP).XMD và XCB (do MQ song song với CB và MD song song với BX).XNC và XAD (do NP song song với AD và NC song song với XA).
Từ tính chất của các tam giác đồng dạng, ta có thể viết các tỉ số tương ứng:
(1)PNMQ=PXQX(1)(2)CBMD=XBXM(2)(3)ADNC=AXNX(3)
Như vậy, từ các phương trình trên, ta có thể suy ra:
(4)PNMQ=CBMD⋅ADNC(4)
Vậy nên ta thấy rằng PNMQ=CBMD⋅ADNC.
Từ (4), ta thấy rằng MQ=PN khi và chỉ khi MD=NC, CB=AD, tức là ABCD là hình vuông.
Do đó, ta đã chứng minh được rằng MN=PQ khi và chỉ khi ABCD là hình vuông.
mong là đúng:))![]()
![]()
![]()