Bài 4: Hai mặt phẳng vuông góc
Các câu hỏi tương tự
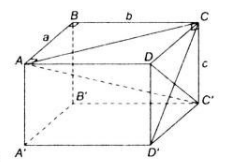
a) Cho hình lập phương ABCD. A'B'C'D' cạnh a. Chứng minh rằng đường thẳng AC' vuông góc với mặt phẳng (A'BD) và mặt phẳng (ACC'A') vuông góc với mặt phẳng (A'BD)
b) Tính đường chéo AC' của hình lập phương đã cho
Cho lập phương ABCD.A'B'C'D'. Chứng minh rằng :
a) Mặt phẳng (AB'C'D) vuông góc với mặt phẳng (BCD'A')
b) Đường thẳng AC' vuông góc với mặt phẳng (A'BD)
Tứ diện SABC có ba đỉnh A, B, C tạo thành tam giác vuông cân đỉnh B và AC 2a, có cạnh SA vuông góc với mặt phẳng (ABC) và SA a
a) Chứng minh mặt phẳng (SAB) vuông góc với mặt phẳng (SBC)
b) Trong mặt phẳng (SAB) vẽ AH vuông góc với SB tại H, chứng minh AHperpleft(SBCright)
c) Tính độ dài đoạn AH
d) Từ trung điểm O của đoạn AC vẽ OK vuông góc với (SBC) cắt (SBC) tại K. Tính độ dài đoạn OK ?
Đọc tiếp
Tứ diện SABC có ba đỉnh A, B, C tạo thành tam giác vuông cân đỉnh B và AC = 2a, có cạnh SA vuông góc với mặt phẳng (ABC) và SA = a
a) Chứng minh mặt phẳng (SAB) vuông góc với mặt phẳng (SBC)
b) Trong mặt phẳng (SAB) vẽ AH vuông góc với SB tại H, chứng minh \(AH\perp\left(SBC\right)\)
c) Tính độ dài đoạn AH
d) Từ trung điểm O của đoạn AC vẽ OK vuông góc với (SBC) cắt (SBC) tại K. Tính độ dài đoạn OK ?
Hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng nhau. Chứng minh rằng \(AC\perp B'D',AB'\perp CD',AD'\perp CB'\). Khi nào mặt phẳng (AA'C'C) vuông góc với mặt phẳng (BB'D'D) ?
Cho tứ diện ABCD có \(\Delta\)ABC vuông tại A, AB=6 , AC=8. \(\Delta\)BCD có độ dài đường cao kẻ từ đỉnh C bằng 8. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABC). Tính góc giữa mặt phẳng (ABD) và (BCD) .
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm I cạnh a và có góc A bằng 60^0, cạnh SCdfrac{asqrt{6}}{2} và SC vuông góc với mặt phẳng (ABCD)
a) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC)
b) Trong tam giác SCA kẻ IK vuông góc với SA tại K. Hãy tính độ dài IK
c) Chứng minh widehat{BKD}90^0 và từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng (SAD)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm I cạnh a và có góc A bằng \(60^0\), cạnh \(SC=\dfrac{a\sqrt{6}}{2}\) và SC vuông góc với mặt phẳng (ABCD)
a) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC)
b) Trong tam giác SCA kẻ IK vuông góc với SA tại K. Hãy tính độ dài IK
c) Chứng minh \(\widehat{BKD}=90^0\) và từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng (SAD)
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn thẳng SO
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD)
Bài 1: Cho hình chóp S ABC . có SA vuông góc (ABC) và đáy ABC vuông ở A.
a. Chứng minh: (SAB) vuông góc (ABC) ; (SAB) vuông góc (SAC)
b. Vẽ AH vuông góc BC, H thuộc BC . Chứng minh : (SBC) vuông góc (SAH)
Bài 2: Cho tứ diện ABCD có AC AD và BC BD . Gọi I là trung điểm của CD .
Chứng minh : (BCD) vuông góc (AIB)
Bài 3: Cho hình hộp chữ nhật ABCD. ABCD . có AB AA a , AD 2a .Gọi M, N, M , N lần lượt là trung
điểm của AD, BC, AD ,BC . Chứng minh :
a. (AAC) vuông góc (ABCD)
b. (MMC) vuông góc...
Đọc tiếp
Bài 1: Cho hình chóp S ABC . có SA vuông góc (ABC) và đáy ABC vuông ở A.
a. Chứng minh: (SAB) vuông góc (ABC) ; (SAB) vuông góc (SAC)
b. Vẽ AH vuông góc BC, H thuộc BC . Chứng minh : (SBC) vuông góc (SAH)
Bài 2: Cho tứ diện ABCD có AC = AD và BC = BD . Gọi I là trung điểm của CD .
Chứng minh : (BCD) vuông góc (AIB)
Bài 3: Cho hình hộp chữ nhật ABCD. A'B'C'D' . có AB = AA = a , AD = 2a .Gọi M, N, M' , N' lần lượt là trung
điểm của AD, BC, A'D' ,B'C' . Chứng minh :
a. (AA'C) vuông góc (ABCD)
b. (MM'C') vuông góc (NDD'N')
II. PHẦN TRẮC NGHIỆM
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Các mặt phẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước thì luôn đi qua một
đường thẳng cố định.
D. Nếu hai mặt phẳng vuông góc với nhau thì bất kì đường thẳng nào nằm trong mặt phẳng này sẽ vuông góc với
mặt phẳng kia.
Câu 3: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có bốn mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
B. Nếu hình hộp có ba mặt bên là hình chữ nhật thì nó là hình hộp chữ nhật.
C. Nếu hình hộp có hai mặt bên cùng vuông góc với mặt đáy thì hình hộp đó là hình hộp đứng.
D. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.
Cho tam giác ABC vuông tại B. Một đoạn thẳng AD vuông góc với mặt phẳng (ABC). Chứng minh rằng mặt phẳng (ABD) vuông góc với mặt phẳng (BCD)
Từ điểm A trong mặt phẳng (ABD) ta vẽ AH vuông góc với BD, chứng minh rằng AH vuông góc với mặt phẳng (BCD) ?