Question

Cho hình chóp A.ABC có 4 đỉnh đều nằm trên một mặt cầu, SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó ?

Answer 1

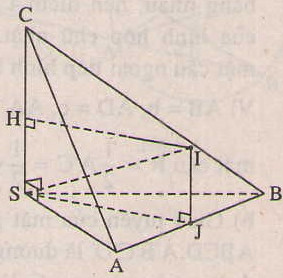
Gọi I là tâm cầu ngoại tiếp hình chóp tam giác S.ABC. Hạ IJ vuông góc (SAB), vì J cách đều 3 điểm S, A, B nên J cũng cách đều 3 điểm S, A, B.

Vì tam giác SAB vuông đỉnh S nên J là trung điểm của AB.

Ta có SJ = .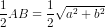

Do SC vuông góc (SAB) nên IJ // SC.

Gọi H là trung điểm SC, ta có SH = IJ = .

Do vậy, IS² = IJ² + SJ² = (a² + b² + c²)/4 và bán kính hình cầu ngoại tiếp S.ABC là

r = IS = .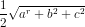

Diện tích mặt cầu là:

S = 4 πr² = π(a² + b² + c²) (đvdt)

Thể tích khối cầu là :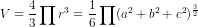 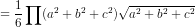(đvtt)