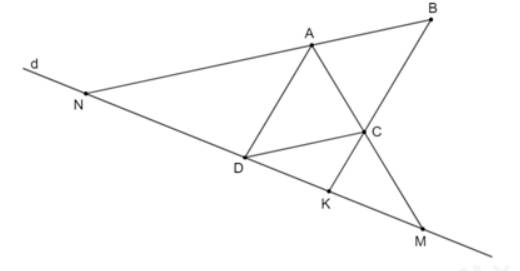
Vì ABCD là hình bình hành nên AB // CD, AD // BC suy ra AN // CD, AD // CK.
Áp dụng định lí Thalès vào tam giác AMN có AN // CD, ta được:
\(\dfrac{{DM}}{{MN}} = \dfrac{{CM}}{{AM}}\) (1)
Áp dụng định lí Thalès vào tam giác ADM có CK // AD, ta được:
\(\dfrac{{MK}}{{DM}} = \dfrac{{CM}}{{AM}}\) (2)
Từ (1) và (2) suy ra: \(\dfrac{{DM}}{{MN}} = \dfrac{{MK}}{{DM}} = \dfrac{{CM}}{{AM}}\)
Do đó DM2 = MN . MK (đpcm).