Cho hình bình hành ABCD có AB = 4, AD = 6, \(\widehat {BAD} = {60^o}\) (Hình 73).
a) Biểu thị các vecto \(\overrightarrow {BD} ,\overrightarrow {AC} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} .\)
b) Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AD} ,\;\overrightarrow {AB} .\overrightarrow {AC} ,\;\overrightarrow {BD} .\overrightarrow {AC} .\)
c) Tính độ dài các đường chéo \(BD,AC.\)
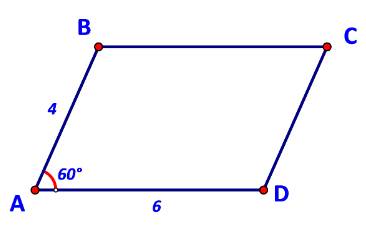
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)