Xét tam giác MNP và tam giác QNP: MN = QN; MP = QP; NP chung.
Vậy \(\Delta MNP = \Delta QNP\) (c.c.c)
Vậy \(\widehat {MNP} = \widehat {QNP}\) ( 2 góc tương ứng)
Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, \(\widehat A = 65^\circ ,\widehat N = 71^\circ \). Tính số đo các góc còn lại của hai tam giác.
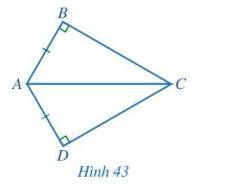
Cho Hình 43 có AB = AD, \(\widehat {ABC} = \widehat {ADC} = 90^\circ \). Chứng minh \(\widehat {ACB} = \widehat {ACD}\).
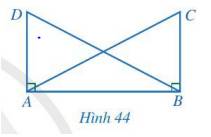
Cho Hình 44 có AC = BD, \(\widehat {ABC} = \widehat {BAD} = 90^\circ \). Chứng minh AD = BC.
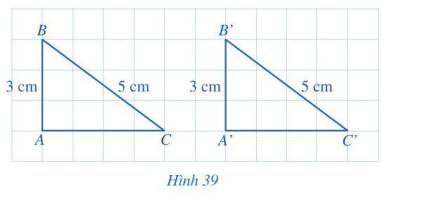
Cho hai tam giác vuông ABC và A’B’C’ có: \(\widehat A = \widehat {A'} = 90^\circ ,AB = A'B' = 3\)cm,\(BC = B'C' = 5\)cm (Hình 39). So sánh độ dài các cạnh AC và A’C’.
Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’, BC = B’C’, CA = C’A’.
Tam giác ABC có bằng tam giác A’B’C’ hay không?
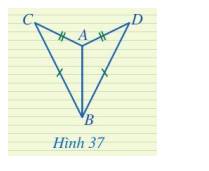
Hai tam giác ở Hình 37 có bằng không? Vì sao?
