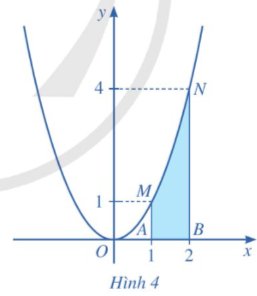
Cho hàm số y = f(x) = x2. Xét hình phẳng (được tô màu) gồm tất cả các điểm M(x; y) trên mặt phẳng tọa độ sao cho 1 ≤ x ≤ 2 và 0 ≤ y ≤ x2 (Hình 4). Hình phẳng đó được gọi là hình thang cong AMNB giới hạn bởi đồ thị của hàm số f(x) = x2, trục Ox và hai đường thẳng x = 1, x = 2.
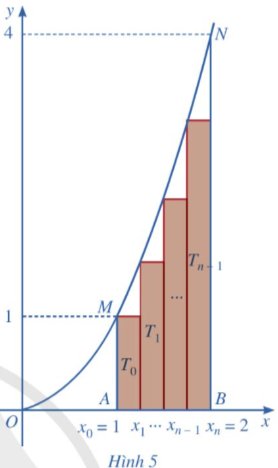
Chia đoạn [1; 2] thành n phần bằng nhau bởi các điểm chia:
\(x_0=1;x_1=1+\dfrac{1}{n};x_2=1+\dfrac{2}{n},...,x_{n-1}=1+\dfrac{n-1}{n},x_n=1+\dfrac{n}{n}=2\) (Hình 5)
a) Tính diện tích T0 của hình chữ nhật dựng trên đoạn [x0; x1] với chiều cao là f(x0).
Tính diện tích T1 của hình chữ nhật dựng trên đoạn [x1; x2] với chiều cao là f(x1).
Tính diện tích T2 của hình chữ nhật dựng trên đoạn [x2; x3] với chiều cao là f(x2).
…
Tính diện tích Tn – 1 của hình chữ nhật dựng trên đoạn [xn – 1; xn] với chiều cao là f(xn–1).
b) Đặt Sn = T0 + T1 + T2 + … + Tn – 1. Chứng minh rằng:
Sn = \(\dfrac{1}{2}\).[f(x0) + f(x1) + f(x2) + … + f(xn – 1)].
Tổng Sn gọi là tổng tích phân cấp n của hàm số f(x) = x2 trên đoạn [1; 2].
a) \({T_0} = f({x_0}).({x_1} - {x_0}) = f(1).({x_1} - 1)\);
\({T_1} = f({x_1}).({x_2} - {x_1})\);
\({T_2} = f({x_2}).({x_3} - {x_2})\);
…
\({T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}})\);
b) \({T_0} = f({x_0}).({x_1} - {x_0}) = f({x_0}).({x_0} + \frac{1}{n} - {x_0}) = \frac{{f({x_0})}}{n}\);
\({T_1} = f({x_1}).({x_2} - {x_1}) = f({x_1}).({x_1} + \frac{1}{n} - {x_1}) = \frac{{f({x_1})}}{n}\);
\({T_2} = f({x_2}).({x_3} - {x_2}) = f({x_2}).({x_2} + \frac{1}{n} - {x_2}) = \frac{{f({x_2})}}{n}\);
…
\({T_{n - 1}} = f({x_{n - 1}}).({x_n} - {x_{n - 1}})\)
\(= f({x_{n - 1}}).({x_{n - 1}} + \frac{1}{n} - {x_{n - 1}}) = \frac{{f({x_{n - 1}})}}{n}\).
Vậy \({S_n} = {T_0} + {T_1} + {T_2} + ... + {T_{n - 1}}\)
\(= \frac{1}{n}[f({x_0}) + f({x_1}) + f({x_2}) + ... + f({x_{n - 1}})]\).


