Cho hai mặt phẳng (P) và (P') có vectơ pháp tuyến lần lượt là \(\overrightarrow{n}=\left(n_1;n_2;n_3\right),\overrightarrow{n'}=\left(n'_1;n'_2;n'_3\right)\) (Hình 14).
Gọi d và d' là hai đường thẳng lần lượt vuông góc với (P) và (P'). Góc giữa hai mặt phẳng (P) và (P') là góc giữa hai đường thẳng d và d'. So sánh cos((P), (P')) và \(\cos\left(\overrightarrow{n},\overrightarrow{n'}\right)\).
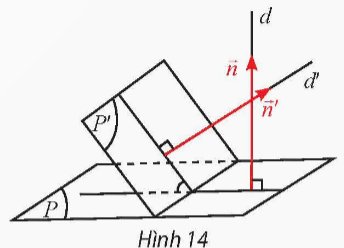
Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\), nên suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) = \left( {d,d'} \right).\)
Như vậy \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \cos \left( {d,d'} \right) = \left| {\cos \left( {\vec n,\vec n'} \right)} \right|\). (Do \(\vec n\) và \(\vec n'\) lần lượt là các vectơ chỉ phương của các đường thẳng \(d\) và \(d'.\)


