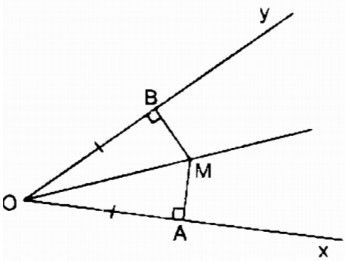
Xét hai tam giác vuông MOA và MOB:
\(\widehat{MAO}=\widehat{MBO}=90^0\)
OA = OB (gt)
OM cạnh huyền chung
Do đó: ∆ MAO = ∆ MBO (cạnh huyền, cạnh góc vuông)
⇒\(\widehat{AOM}=\widehat{BOM}\)
A và B thay đổi, OA và OB luôn bằng nhau nên ∆ MAO và ∆ MBO luôn luôn bằng nhau do đó \(\widehat{AOM}=\widehat{BOM}\)
Vậy khi A chuyển động trên Ox, B chuyển động trên Oy mà OA = OB thì điểm M chuyển động trên tia phân giác của góc xOy.








