Question

Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat {ABN} = \widehat {ACM}\)

a) Chứng minh rằng ΔABN ∽ ΔACM

b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN=IC.IM

Answer 1

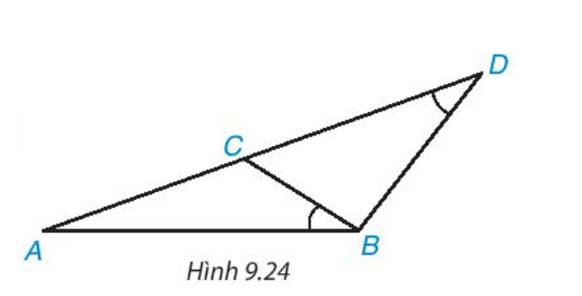
a) Xét tam giác ABN và tam giác ACM

có góc A chung, \(\widehat {ABN} = \widehat {ACM}\)

=> ΔABN ∽ ΔACM

b) Có ΔABN ∽ ΔACM

\(\widehat {ANB} = \widehat {AMC}\)

Có \(\widehat {ANB} + \widehat {CNB} = {180^o}\)

     \(\widehat {AMC} + \widehat {BMC} = {180^o}\)

=> \(\widehat {CNB} = \widehat {BMC}\)

Xét tam giác IBM và tam giác ICN 

Có \(\widehat {CNB} = \widehat {BMC}\) và \(\widehat {IBM} = \widehat {ICN}\)

  => ΔIBM ∽ ΔICN (g.g)

=> \(\frac{{IB}}{{IC}} = \frac{{IM}}{{IN}}\)

=> IB.IN=IC.IM