Cho góc AIB nội tiếp đường tròn tâm O đường kính IK sao cho tâm O nằm trong góc đó (Hình 57).
a) Các cặp góc $\widehat{O A I}$ và $\widehat{O I A} ; \widehat{O B I}$ và $\widehat{O I B}$ có bằng nhau hay không?
b) Tính các tổng $\widehat{A O I}+2 \widehat{O I A}, \widehat{B O I}+2 \widehat{O I B}$.
c) Tính các tổng $\widehat{A O I}+\widehat{A O K}, \widehat{B O I}+\widehat{B O K}$.
d) So sánh $\widehat{A O K}$ và $\widehat{2 O I A}, \widehat{B O K}$ và $2 \widehat{O I B}, \widehat{A O B}$ và $2 \widehat{A I B}$.
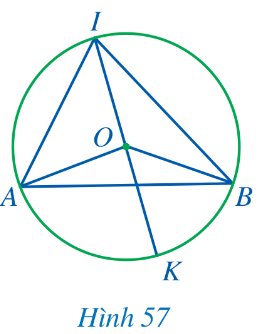
a) Do \(OI = OA = R\) nên tam giác \(IOA\) cân tại \(O\) suy ra \(\widehat {OAI} = \widehat {OIA}\)
Do \(OI = OB = R\) nên tam giác \(IOB\) cân tại \(O\) suy ra \(\widehat {OBI} = \widehat {OIB}\)
b) Xét tam giác \(AOI\) cân tại \(O\) có:
\(\widehat {AOI} + \widehat {OIA} + \widehat {OAI} = 180^\circ \Rightarrow \widehat {AOI} + \widehat {OIA} + \widehat {OIA} = 180^\circ \Rightarrow \widehat {AOI} + 2\widehat {OIA} = 180^\circ \)
Xét tam giác \(BOI\) cân tại \(O\) có:
\(\widehat {BOI} + \widehat {OIB} + \widehat {OBI} = 180^\circ \Rightarrow \widehat {BOI} + \widehat {OIB} + \widehat {OIB} = 180^\circ \Rightarrow \widehat {BOI} + 2\widehat {OIB} = 180^\circ \)
c) Ta có: \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) (hai góc kề bù)
\(\widehat {BOI} + \widehat {BOK} = 180^\circ \) (hai góc kề bù)
d) Do \(\widehat {AOI} + 2\widehat {OIA} = 180^\circ \) lại có \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) nên \(2\widehat {OIA} = \widehat {AOK}\)
Do \(\widehat {BOI} + 2\widehat {OIB} = 180^\circ \) lại có \(\widehat {BOI} + \widehat {BOK} = 180^\circ \) nên \(2\widehat {OIB} = \widehat {BOK}\)
Ta có: \(\widehat {OIA} + \widehat {OIB} = \widehat {AIB} \Rightarrow 2\left( {\widehat {OIA} + \widehat {OIB}} \right) = 2\widehat {AIB} \Rightarrow 2\widehat {OIA} + 2\widehat {OIB} = 2\widehat {AIB}\)
Mà \(2\widehat {OIA} = \widehat {AOK},2\widehat {OIB} = \widehat {BOK}\) nên \(\widehat {AOK} + \widehat {BOK} = 2\widehat {AIB} \Rightarrow \widehat {AOB} = 2\widehat {AIB}\)


