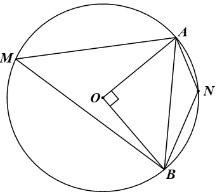
a) Áp dụng định lí Pythagore vào tam giác \(AOB\) vuông tại \(O\), ta có:
\(O{A^2} + O{B^2} = A{B^2} \Rightarrow A{B^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow AB = R \sqrt 2\)
b) Xét đường tròn \(\left( O \right)\):
+) Vì M thuộc cung lớn AB nên \(\widehat {AMB}\) là góc nội tiếp và \(\widehat {AOB}\) là góc ở tâm cùng chắn cung nhỏ \(AB\) nên:
\(\widehat {AMB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.90^\circ = 45^\circ \).
+) Số đo cung lớn AB là:
$sđ\overset\frown{AB}\; lớn=360{}^\circ - sđ\overset\frown{AB }\; nhỏ=360{}^\circ -90{}^\circ =270{}^\circ $
+) Vì N thuộc cung nhỏ AB nên \(\widehat {ANB}\) là góc nội tiếp chắn cung lớn \(AB\) nên:
$\widehat{ANB}=\frac{1}{2}sđ\overset\frown{AB }\; lớn=\frac{1}{2}.270{}^\circ =135{}^\circ $.
Vậy \(\widehat {AMB} = 45^\circ ,\widehat {ANB} = 135^\circ \).


