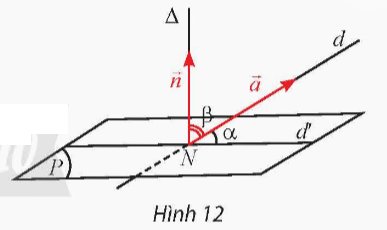
Cho đường thẳng d có vectơ chỉ phương \(\overrightarrow{a}\) = (a1; a2; a3) và mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow{n}\) = (n1; n2; n3). Biết d cắt (P) tại điểm N và hình chiếu vuông góc của d lên (P) là đường thẳng d'. Qua N vẽ đường thẳng D vuông góc với (P) (Hình 12).
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.
b) Có nhận xét gì về số đo của hai góc α = (d, d'); β = (D, d)?
c) Giải thích tại sao ta lại có đẳng thức: \(\sin\left(d,\left(P\right)\right)=\left|\cos\left(\overrightarrow{a},\overrightarrow{n}\right)\right|\).
a) Nếu đường thẳng \(a\) vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là \({90^o}\).
Nếu đường thẳng \(a\) không vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(a\) và hình chiếu \(a'\) của \(a\) trên \(\left( P \right).\)
b) Nhìn vào hình vẽ, ta thấy rằng hai góc \(\alpha \) và \(\beta \) có tổng số đo là \({90^o}.\)
c) Do \(\alpha + \beta = {90^o}\) nên ta có \(\sin \alpha = \cos \beta .\)
Ta có \(d'\) là hình chiếu vuông góc của \(d\) lên \(\left( P \right)\), nên \(\alpha = \left( {d,d'} \right) = \left( {d,\left( P \right)} \right).\)
Ta có \(\beta = \left( {\Delta ,d} \right)\) nên \(\cos \beta = \cos \left( {\Delta ,d} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|\). (Vì \(\vec a\) và \(\vec n\) lần lượt là các vectơ chỉ phương của các đường thẳng \(d\) và \(\Delta \)).
Mà \(\sin \alpha = \cos \beta \) nên \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)


