Bài 4: Bất phương trình bậc nhất một ẩn.
Các câu hỏi tương tự
Cho bất phương trình ẩn \(x\) :
\(2x+1>2\left(x+1\right)\)
a) Chứng tỏ các giá trị \(-5;0;-8\) đều không phải là nghiệm của nó ?
b) Bất phương trìh này có thể nhận những giá trị nào của ẩn \(x\) là nghiệm ?
Cho bất phương trình \(x^2>0\) :
a) Chứng tỏ \(x=2;x=-3\) là nghiệm của bất phương trình đã cho
b) Có phải mọi giá trị của ẩn \(x\) đều là nghiệm của bất phương trình đã cho không ?
Với giá trị nào của \(m\) thì phương trình ẩn \(x\)
a) \(x-2=3m+4\) có nghiệm lớn hơn 3
b) \(3-2x=m-5\) có nghiệm nhỏ hơn -2
Với giá trị nào của \(m\) thì phương trình ẩn \(x\) :
a) \(x-3=2m+4\) có nghiệm dương
b) \(2x-5=m+8\) có nghiệm âm
Đố :
Kiểm tra xem giá trị \(x=-2\) có là nghiệm của bất phương trình sau không ?
a) \(x+2x^2-3x^3+4x^4-5< 2x^2-3x^3+4x^4-6\)
b) \(\left(-0,001\right)x>0,003\)
Đố :
Tìm sai lầm trong các lời giải sau :
a) Giải bất phương trình -2x23. Ta có :
-2x23Leftrightarrow x23+2Leftrightarrow x25
Vậy nghiệm của bất phương trình là : x25
b) Giải bất phương trình -dfrac{3}{7}x12. Ta có :
-dfrac{3}{7}x12Leftrightarrowleft(-dfrac{7}{3}right).left(-dfrac{3}{4}xright)left(-dfrac{7}{3}right).12Leftrightarrow x-28
Vậy nghiệm của bất phương trình là x-28
Đọc tiếp
Đố :
Tìm sai lầm trong các "lời giải" sau :
a) Giải bất phương trình \(-2x>23\). Ta có :
\(-2x>23\Leftrightarrow x>23+2\Leftrightarrow x>25\)
Vậy nghiệm của bất phương trình là : \(x>25\)
b) Giải bất phương trình \(-\dfrac{3}{7}x>12\). Ta có :
\(-\dfrac{3}{7}x>12\Leftrightarrow\left(-\dfrac{7}{3}\right).\left(-\dfrac{3}{4}x\right)>\left(-\dfrac{7}{3}\right).12\Leftrightarrow x>-28\)
Vậy nghiệm của bất phương trình là \(x>-28\)
Hãy cho biết số nào trong các số \(\dfrac{2}{3};\dfrac{2}{7};-\dfrac{4}{5}\) là nghiệm của bất phương trình :
\(5-3x< \left(4+2x\right)-1\)
giải bất phương trình và biểu diễn tập nghiệm:
c) 2x - 8 \(\ge\) 2\(\times\) ( x + 1/2)
d) \(\dfrac{5x^2-3x}{5}+\dfrac{3x+1}{4}< \dfrac{x\left(2x+1\right)}{2}-\dfrac{3}{2}\)
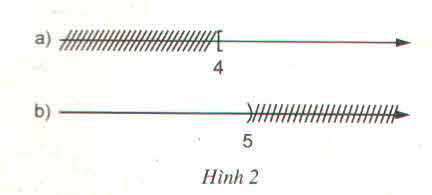
Viết bất phương trình bậc nhất một ẩn có tập nghiệm biểu diễn bởi hình vẽ sau (h.2)