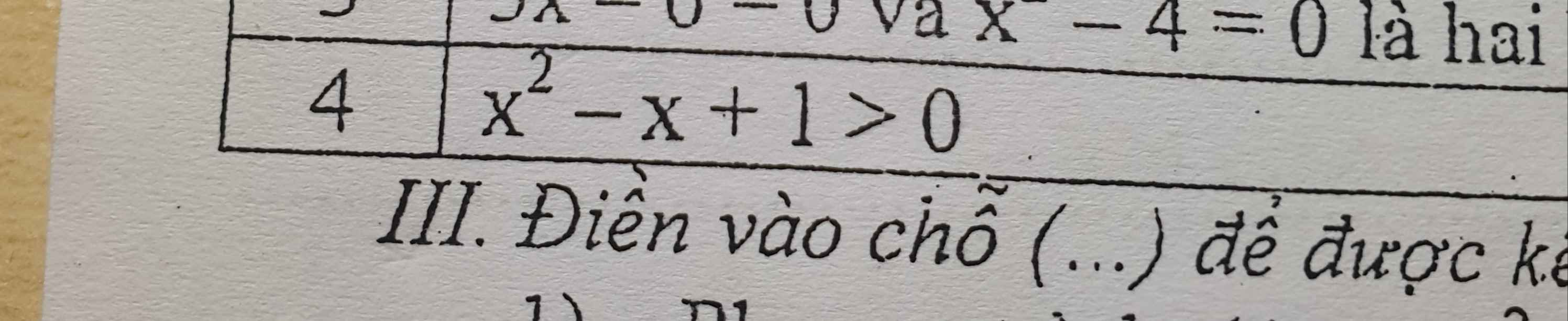\(x^2-x+1=x^2-2.\dfrac{1}{2}.x+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{2}\right)^2+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)
--> Đúng
\(\Leftrightarrow x\left(x-1\right)+1>0\)
vì \(x\left(x-1\right)\ge0\)
mà 1 > 0
\(=>x\left(x-1\right)+1>0\)
hay \(x^2-x+1>0\left(đúng\right)\)
`<=> x(x - 1) + 1 > 0`
Vì `x(x - 1) >= 0`
Mà `1 > 0`
`=> x(x - 1) + 1 > 0`
Hay `x^2 - x + 1 > 0` (luôn đúng)
`=>` Ta có:
`x^2 - x + 1 = x^2 - 2 . 1/2 . x + (1/2)^2 - (1/2)^2 + 1 = (x - 1/2)^2 + 3/4 >= 3/4 > 0` (luôn đúng)