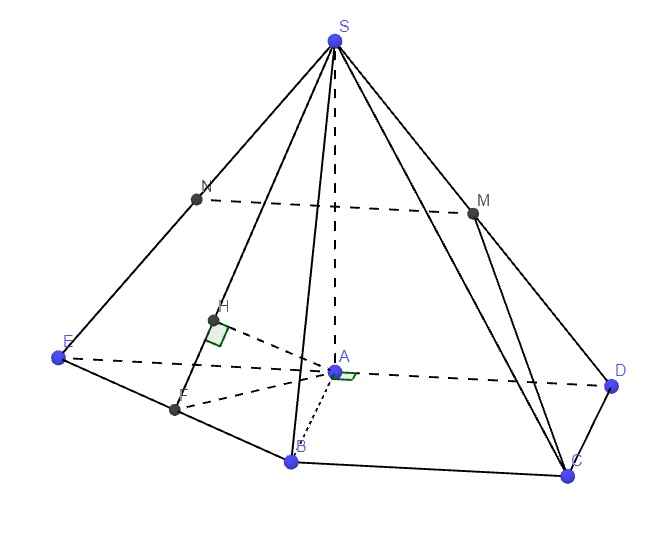
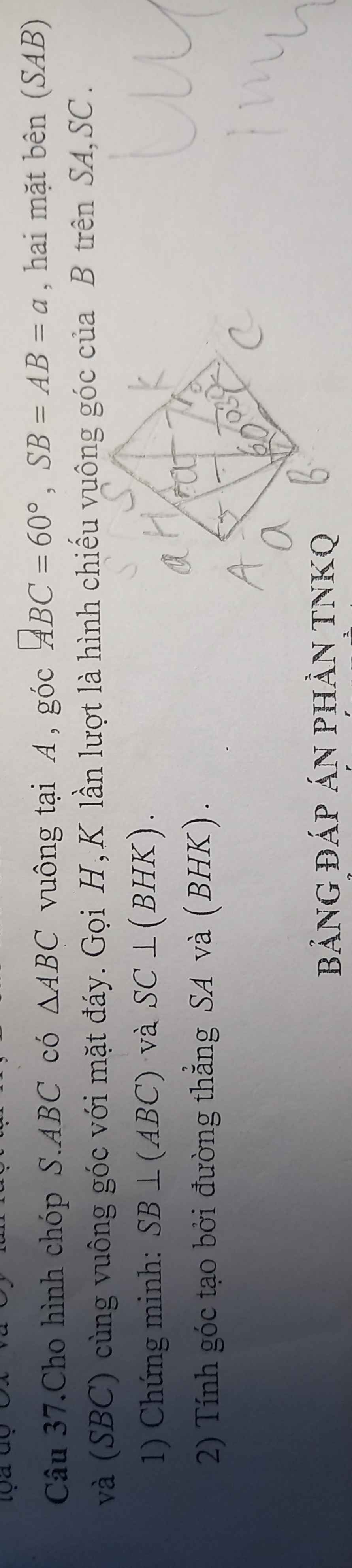a.
Đề sai, \(\left(BMD\right)\) và \(\left(ABCD\right)\) không hề vuông góc (mặt phẳng (BMD) trong trường hợp này trùng mặt phẳng (SBD), mà (SBD) và (ABCD) không hề vuông góc
Đề bài chỉ đúng khi M là trung điểm SC
b.
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=a\sqrt{2}\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{2}\Rightarrow\widehat{SCA}\approx54^044'\)
c.
Gọi E là điểm đối xứng D qua A, N là trung điểm SE
\(\Rightarrow BCMN\) là hình bình hành
\(\Rightarrow CM||BN\Rightarrow CM||\left(SBE\right)\Rightarrow d\left(CM;SB\right)=d\left(CM;\left(SBE\right)\right)=d\left(M;\left(SBE\right)\right)\)
Lại có AM là đường trung bình tam giác SDE
\(\Rightarrow AM||SE\Rightarrow AM||\left(SDE\right)\Rightarrow d\left(M;\left(SDE\right)\right)=d\left(A;\left(SDE\right)\right)\)
Gọi F là trung điểm BE, từ A kẻ AH vuông góc SF (H thuộc SF)
\(\Delta ABE\) vuông cân tại A \(\Rightarrow\left\{{}\begin{matrix}AF\perp BE\\AF=\dfrac{1}{2}BE=\dfrac{a\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow BE\perp\left(SAF\right)\Rightarrow BE\perp AH\)
\(\Rightarrow AH\perp\left(SBE\right)\Rightarrow AH=d\left(A;\left(SBE\right)\right)\)
Hệ thức lượng: \(AH=\dfrac{SA.AF}{\sqrt{SA^2+AF^2}}=\dfrac{2a}{3}\)
Hay \(d\left(SB;CM\right)=\dfrac{2a}{3}\)