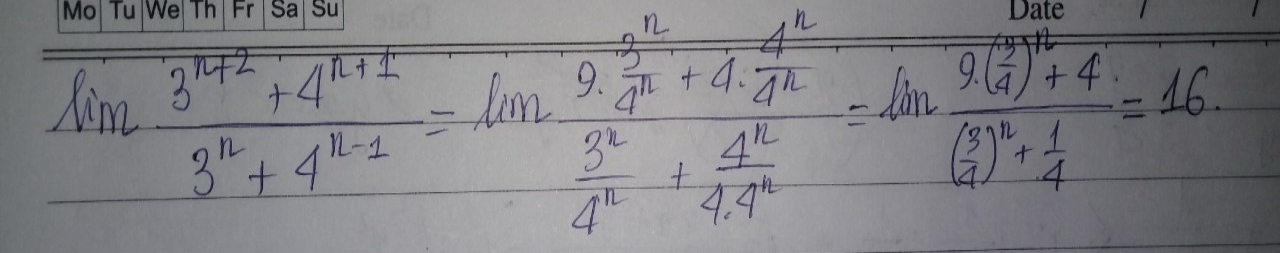Bài 1: Giới hạn của dãy số
Các câu hỏi tương tự
Giúp em câu này vovới ạ
mọi người giúp mình câu này với ^^
Xem chi tiết
1/ lim \(\frac{n^2-2n}{n^2-n+6}\)
2/ lim \(\frac{4n^2-6}{n^4+n^2-17}\)
3/ lim \(\frac{n^3-n^2+n}{n+7}\)
4/ lim \(\frac{\left(3-2n\right)^4}{\left(n+1\right)^2\left(n^2+1\right)}\)
Giúp em giải chi tiết câu 7 , 8 đi ạ em cảm ơn
Giúp em giải chi tiết câu 19 và 20 đi ạ em cảm ơn
17/lim\(\left(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{\left(2n-1\right)\left(2n+1\right)}\right)\)
18/lim\(\frac{1+a+a^2+...+a^n}{1+b+b^2+...+b^n}\left(\left|a\right|< 1;\left|b\right|< 1\right)\)
19/lim\(\frac{1-2+3-4+...+\left(2n-1\right)-2n}{2n+1}\)
Chào mọi người, em đang bí câu này, mong được sự giúp đỡ gợi ý từ thầy cô và các bạn ạ, em cảm ơn. <3
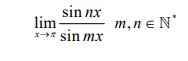
Dùng kết quả của câu 1.7 để tính giới hạn của các dãy số có số hạng tổng quát như sau :
a) \(u_n=\dfrac{1}{n!}\)
b) \(u_n=\dfrac{\left(-1\right)^n}{2n-1}\)
c) \(u_n=\dfrac{2-n\left(-1\right)^n}{1+2n^2}\)
d) \(u_n=\left(0,99\right)^n\cos n\)
e) \(u_n=5^n-\cos\sqrt{n}\pi\)
Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau 1 khoảng thời gian T24000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã)
Gọi u_n là khối lượng chất phóng xạ còn lại sau chu kì thứ n
a) Tìm số hạng tổng quát u_n của dãy số left(u_nright)
b) Chứng minh rằng left(u_nright) có giới hạn là 0
c) Từ kết quả của câu b), chứng tỏ rằng sau một số năm nào đó, khối lượng chất phóng xạ đã cho ban đầu không còn độ...
Đọc tiếp
Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau 1 khoảng thời gian \(T=24000\) năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã)
Gọi \(u_n\) là khối lượng chất phóng xạ còn lại sau chu kì thứ n
a) Tìm số hạng tổng quát \(u_n\) của dãy số \(\left(u_n\right)\)
b) Chứng minh rằng \(\left(u_n\right)\) có giới hạn là 0
c) Từ kết quả của câu b), chứng tỏ rằng sau một số năm nào đó, khối lượng chất phóng xạ đã cho ban đầu không còn độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \(10^{-6}g\)