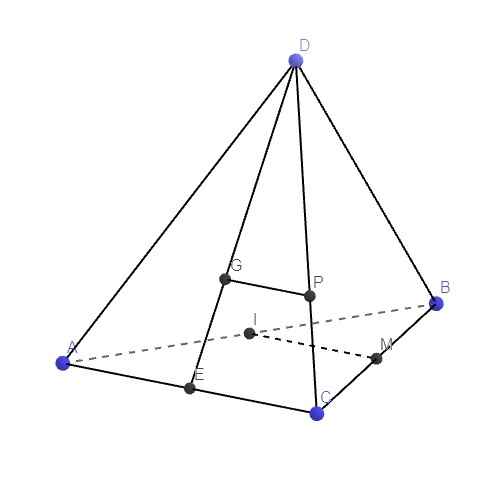
Gọi E là trung điểm AC, do G là trọng tâm tam giác ACD \(\Rightarrow G\in DE\)
Theo t/c trọng tâm: \(\dfrac{GE}{GD}=\dfrac{1}{2}\)
Do I là trung điểm AB, M là trung điểm BC \(\Rightarrow\) IM là đường trung bình tam giác ABC
\(\Rightarrow IM||AC\)
Qua G kẻ đường thẳng song song AC cắt CD tại P
\(\left\{{}\begin{matrix}G\in\left(IGM\right)\\GP||AC||IM\end{matrix}\right.\) \(\Rightarrow P\in\left(IGM\right)\)
\(\Rightarrow P=CD\cap\left(IGM\right)\)
Theo định lý Talet: \(\dfrac{PC}{PD}=\dfrac{GE}{GD}=\dfrac{1}{2}\)
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M và N lần lượt là trung điểm của SA và
SC. Tìm giao điểm K của đường thẳng SD với mặt phẳng (BMN) và tính tỷ số SK/SD