Xét tam giác ABC có: \(AC + CB > AB\).
Vậy nên bạn Hoa đi đường thứ nhất đi từ A đến C và đi tiếp từ C đến B sẽ dài hơn đi đường thứ hai đi từ B đến A.
Bạn Hoa vẽ tam giác ABC lên tờ giấy sau đó cắt một phần tam giác ở phía góc A (Hình 145). Bạn Hoa đố bạn Hùng: Không vẽ điểm A, làm thế nào tìm được điểm D trên đường thẳng BC sao cho khoảng cách từ D đến điểm A là nhỏ nhất? Em hãy giúp bạn Hùng tìm cách vẽ điểm D và giải thích cách làm của mình?
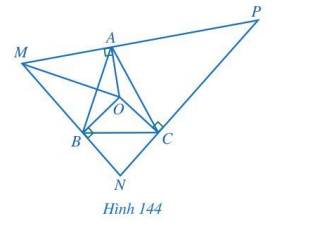
Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144). Chứng minh:
a) \(\Delta OMA = \Delta OMB\) và tia MO là tia phân giác của góc NMP;
b) O là giao điểm của ba đường phân giác của tam giác MNP.
Cho hai tam giác nhọn ABC và ECD, trong đó ba điểm B, C, D thẳng hàng. Hai đường cao BM và CN của tam giác ABC cắt nhau tại I, hai đường cao CP và DQ của tam giác ECD cắt nhau tại K (Hình 143). Chứng minh AI // EK.
Cho tam giác ABC có BC > AC, I là giao điểm của hai đường phân giác góc A và góc B. Khi đó
A.\(\widehat {ICA} = \widehat {ICB}\). B.\(\widehat {IAC} = \widehat {IBC}\). C.\(\widehat {ICA} > \widehat {ICB}\). D.\(\widehat {ICA} < \widehat {IBC}\).
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Khi đó
A.\(AM = 2GM\). B.\(AM = 2AG\). C.\(GA = 3GM\). D.\(GA = 2GM\).
Cho tam giác ABC cân tại A có \(\widehat {BAC} = 40^\circ \). Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Khi đó
A.\(OA = OB = AB\). B.\(OA = OB = OC\). C.\(OB = OC = BC\). D.\(OC = OA = AC\).
Cho tam giác nhọn ABC có AB < AC. Hai đường cao AD và CE cắt nhau tại H. Khi đó
A.\(\widehat {HAB} = \widehat {HAC}\).
B.\(\widehat {HAB} > \widehat {HAC}\).
C.\(\widehat {HAB} = \widehat {HCB}\).
D.\(\widehat {HAC} = \widehat {BAC}\).
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Các điểm A, G, H, I, O phân biệt. Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng;
b) Nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
Cho Hình 142 có O là trung điểm của đoạn thẳng AB và O nằm giữa hai điểm M, N. Chứng minh:
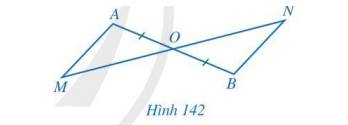
a) Nếu OM = ON thì AM // BN;
b) Nếu AM // BN thì OM = ON.
