Hình 47)
x+ 900 + 550 = 1800
=> x= 1800 – ( 900+ 550)= 350
Hình 48)
x+ 400 + 300= 1800
=> x= 1800 – ( 400+ 390)= 1100
Hình 49)
x+ x + 500= 1800
=> 2x= 1800 – 500=1300
x= 650
Hình50)
y= 600+ 400= 1000
y+ 400= 1800 (kề bù)
x= 1800 – 400 = 1400
Hình 51)
Trong ∆ ABC có
(400+ 400) + 700+ y = 1800
y+ 1500= 1800
y= 1800 - 1500= 300
Trong ∆ ACD có:
x+ 400 + 300= 1800
x= 1800 – ( 400+ 400)= 1100
Giải:
Hình 47)
x+ 900 + 550 = 1800
=> x= 1800 – ( 900+ 550)= 350
Hình 48)
x+ 400 + 300= 1800
=> x= 1800 – ( 400+ 390)= 1100
Hình 49)
x+ x + 500= 1800
=> 2x= 1800 – 500=1300
x= 650
Hình50)
y= 600+ 400= 1000
y+ 400= 1800 (kề bù)
x= 1800 – 400 = 1400
Hình 51)
Trong ∆ ABC có
(400+ 400) + 700+ y = 1800
y+ 1500= 1800
y= 1800 - 1500= 300
Trong ∆ ACD có:
x+ 400 + 300= 1800
x= 1800 – ( 400+ 400)= 1100
Bài 2. Cho tam giác ABC ˆBB^= 800, ˆCC^= 300. Tia phân giác của góc A cắt BC ở D. Tính ˆADC,ˆADBADC^,ADB^.
Giải:
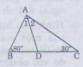
ˆBACBAC^= 1800 - (ˆBB^+ˆCC^) = 1800 - ( 800 + 300)= 700
ˆA1A1^=ˆA2A2^=ˆA2A^2=70027002= 350
ˆADCADC^=ˆBB^+ˆA1A1^(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó ˆADBADB^= 1800 - ˆADCADC^= 1800 + 1150=650










 c hình vẽ sau
c hình vẽ sau


