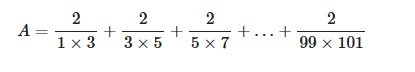\(A=\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{99\times101}\)
\(A=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{2}{99}-\dfrac{2}{101}\)
\(A=1-\left(\dfrac{1}{3}-\dfrac{1}{3}\right)-\left(\dfrac{1}{5}-\dfrac{1}{5}\right)-\left(\dfrac{1}{7}-\dfrac{1}{7}\right)-...-\left(\dfrac{1}{99}-\dfrac{1}{99}\right)-\dfrac{1}{101}\)
\(A=1-0-0-0-...-\dfrac{1}{101}\)
\(A=1-\dfrac{1}{101}\)
\(A=\dfrac{101}{101}-\dfrac{1}{101}\)
\(A=\dfrac{100}{101}\)
A=1−13+13−15+15−17+...+299−2101�=1−13+13−15+15−17+...+299−2101
A=1−0−0−0−...−1101�=1−0−0−0−...−1101
A=101101−1101�=101101−1101