a) Xét dấu đạo hàm của hàm số trên các khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( {1; + \infty } \right)\). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu của đạo hàm trên mỗi khoảng này.
b) Có nhận xét gì về đạo hàm y’ của hàm số y trên khoảng \(\left( { - 1;1} \right)\)?
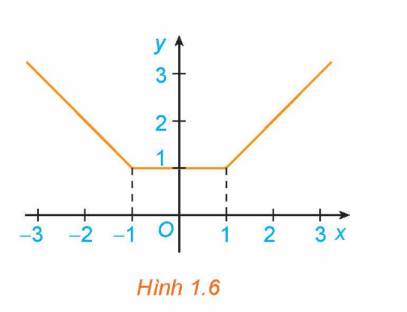
a) + Xét khoảng \(\left( { - \infty ; - 1} \right)\) ta có: \(y' = \left( { - x} \right)' = - 1 < 0\)
Trong khoảng \(\left( { - \infty ; - 1} \right)\) ta thấy hàm số y nghịch biến và đạo hàm \(y' < 0\).
+ Xét khoảng \(\left( {1; + \infty } \right)\) ta có: \(y' = x' = 1 > 0\)
Trong khoảng \(\left( {1; + \infty } \right)\) ta thấy hàm số y đồng biến và đạo hàm \(y' > 0\).
b) Trong khoảng \(\left( { - 1;1} \right)\) ta có: \(y' = \left( 1 \right)' = 0\)
Trong khoảng \(\left( { - 1;1} \right)\) ta thấy hàm số y không đổi và đạo hàm \(y' = 0\).




