Question

a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r, quanh trục Ox (H.4.28).

b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.

Answer 1

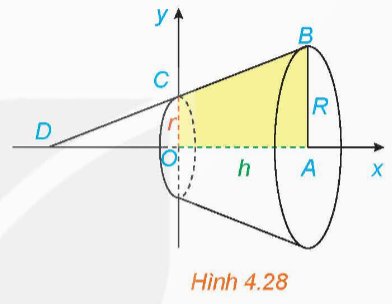
a)

Ta có: \(C\left( {0;r} \right),B\left( {h,R} \right) \Rightarrow \overrightarrow {BC} \left( { - h,r - R} \right) \Rightarrow \overrightarrow n \left( {r - R,h} \right)\)

Phương trình đường thẳng BC là: \(\left( {r - R} \right)x + h\left( {y - r} \right) = 0 \Leftrightarrow y = \frac{{hr + \left( {R - r} \right)x}}{h}\)

Thể tích hình cần tính là:

\(V = \pi \int\limits_0^h {{{\left[ {\frac{{hr + \left( {R - r} \right)x}}{h}} \right]}^2}dx}  = \pi \int\limits_0^h {{{\left[ {r + \frac{{\left( {R - r} \right)x}}{h}} \right]}^2}dx}  = \pi \int\limits_0^h {\left[ {{r^2} + \frac{{2r\left( {R - r} \right)x}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^2}}}{{{h^2}}}} \right]dx} \)

\( = \pi \left( {{r^2}x + \frac{{r\left( {R - r} \right){x^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{x^3}}}{{3{h^2}}}} \right)\left| \begin{array}{l}h\\0\end{array} \right. = \pi \left( {{r^2}h + \frac{{r\left( {R - r} \right){h^2}}}{h} + \frac{{{{\left( {R - r} \right)}^2}{h^3}}}{{3{h^2}}}} \right)\)

\( = \pi \left( {{r^2}h + r\left( {R - r} \right)h + \frac{{{{\left( {R - r} \right)}^2}h}}{3}} \right) = \pi \left( {{r^2}h + rRh - {r^2}h + \frac{{{R^2}h}}{3} - \frac{{2rRh}}{3} + \frac{{{r^2}h}}{3}} \right)\)

\( = \pi \left( {\frac{{rRh}}{3} + \frac{{{R^2}h}}{3} + \frac{{{r^2}h}}{3}} \right) = \frac{1}{3}\pi h\left( {{R^2} + rR + {r^2}} \right)\)

b) Khi \(r = 0\) thì khối nón cụt trở thành khối nón có chiều cao h và bán kính đáy R. Do đó, thể tích khối nón là: \(V = \frac{1}{3}\pi {R^2}h\).