a)
b) 3 cách gọi tên đường thẳng là: AB, BD, CD
Chú ý: Ta có thể gọi tên đường thẳng bằng cách chọn ra hai điểm thuộc đường thẳng: AB, AC, AD, BC, BD, BA, CD, CB, CA, DA, DB, DC.
a)

b) 3 cách gọi tên đường thẳng là: AB, BD, CD
Chú ý: Ta có thể gọi tên đường thẳng bằng cách chọn ra hai điểm thuộc đường thẳng: AB, AC, AD, BC, BD, BA, CD, CB, CA, DA, DB, DC.
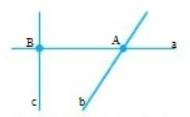
a) Kể tên các đường thẳng có trong Hình 4a.
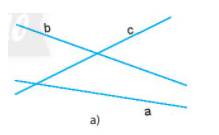
b) Vẽ vào vở ba điểm như Hình 4b. Vẽ các đường thẳng đi qua hai trong ba điểm đó.
c) Từ một tờ giấy A4, em hãy nêu một số cách gấp để tạo ra hình ảnh của điểm và đường thẳng.

- Em hãy đọc tên các điểm có trên hình bên.
- Em hãy vẽ ba điểm vào vở và đặt tên cho ba điểm đó.

Hãy nêu một số hình ảnh của đường thẳng và điểm thuộc (không thuộc) đường thẳng trong thực tế.
Dùng kí hiệu để biểu thị các mối quan hệ dưới đây và vẽ các hình tương ứng.
a) Các điểm A, B thuộc đường thẳng p.
b) Các điểm C, D không thuộc đường thẳng p.
Vẽ hình cho mỗi trường hợp sau:
a) Điểm M thuộc đường thẳng a.
b) Điểm M thuộc hai đường thẳng a và b nhưng không thuộc đường thẳng c.
c) Điểm M nằm trên cả ba đường thẳng a, b và c.
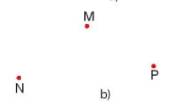
Từ các điểm M, N, P, Q phân biệt như Hình 6, Có thể tạo thành bao nhiêu đường thẳng? Em hãy vẽ các điểm M, N, P, Q vào vở rồi dùng thước và bút để vẽ các đường thẳng đó.
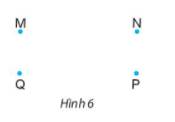
Trong hình vẽ bên:
a) Điểm B thuộc những đường thẳng nào?
b) Điểm A không thuộc những đường thẳng nào?
Sử dụng kí hiệu để mô tả các quan hệ trên.

Điểm A thuộc và không thuộc đường thẳng nào trong hình bên? Dùng các kí hiệu \( \in \) và \( \notin \) để mô tả điều đó.
Có bao nhiêu đường thẳng đi qua hai điểm A, B nói trên.