Bài 4: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
Các câu hỏi tương tự
Trên hình 90 :
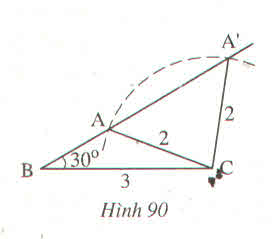
Các tam giác ABC và A'BC có cạnh chung BC = 3cm, CA = CA' = 2cm, \(\widehat{ABC}=\widehat{A'BC}=30^0\) nhưng hai tam giác đó không bằng nhau.
Tại sao ở đây không thể áp dụng trường hợp cạnh - góc - cạnh để kết luận \(\Delta ABC=\Delta A'BC\) ?
3. Chứng minh rằng nếu hai cạnh và trung tuyến thuộc cạnh thứ ba của tam giác này bằnghai cạnh và trung tuyến thuộc cạnh thứ ba của tam giác kia thì hai tam giác này bằng nhau
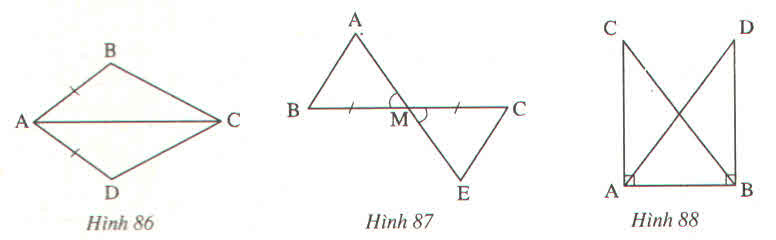
Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây là hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh :
a) \(\Delta ABC=\Delta ADC\) (h.86)
b) \(\Delta AMB=\Delta EMC\) (h.87)
c) \(\Delta CAB=\Delta DBA\) (h.88)
Qua trung điểm I của đoạn thẳng AB, kẻ đường vuông góc với AB, trên đường vuông góc đó lấy hai điểm C và D. Nối CA, CB, DA, DB. Tìm các cặp tam giác bằng nhau trong hình vẽ ?
Dựa vào hình dưới, hãy nêu đề toán chứng minh ΔAOCΔBOC theo trường hợp cạnh-góc-cạnh.
Đọc tiếp
Dựa vào hình dưới, hãy nêu đề toán chứng minh ΔAOC=ΔBOC theo trường hợp cạnh-góc-cạnh.
chứng minh rằng nếu 2 cạnh và trung tuyến thuộc cạnh thứ 3 của tam giác này bằng hai cánh và trung tuyến thuộc cạnh thứ 3 của tam giác kia thì 2 tam giác đó bằng nhau
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC ( H thuộc BC). Các tam giác AHC và BAC có AC là cạnh chung, góc C là góc chung, góc AHC = góc BAC = 90 độ, nhưng hai tam giác đó không bằng nhau. Tại sao ở đây không thể áp dụng trường hợp góc - cạnh - góc để kết luận \(\Delta\)AHC = \(\Delta\)BAC ?
Dựa vào hình 53, hãy nêu đề toán chứng minh \(\Delta AOC=\Delta BOC\) theo trường hợp cạnh - góc - cạnh ?

Bài 12. Cho hai đoạn thẳng AB, CD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn. Chứng minh rằng các đoạn thẳng AC, CB, BD, DA bằng nhau







