Bài 4: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
Các câu hỏi tương tự
Dựa vào hình 53, hãy nêu đề toán chứng minh \(\Delta AOC=\Delta BOC\) theo trường hợp cạnh - góc - cạnh ?

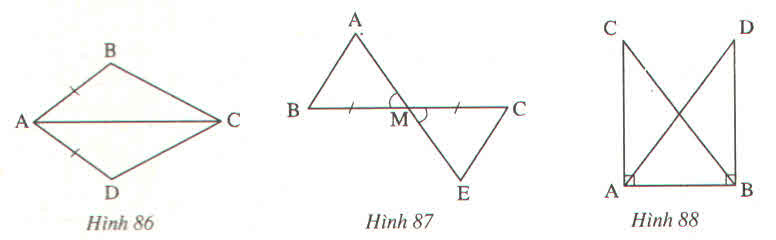
Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây là hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh :
a) \(\Delta ABC=\Delta ADC\) (h.86)
b) \(\Delta AMB=\Delta EMC\) (h.87)
c) \(\Delta CAB=\Delta DBA\) (h.88)
Cho tam giác ABC; AB = AC, D là điểm bất kì trên cạnh AB. Đường phân giác của góc A cắt cạnh DC tại M, cắt cạnh BC tại I.
a) Chứng minh: CM = BM
b) Kẻ DH vuông góc với BC tại H. Chứng minh: A = 2BDH.
Cho hình bs.2
Trong các khẳng định sau, khẳng định nào đúng ? khẳng định nào sai ?
Bổ sung thêm điều kiện sau thì Delta ACDDelta DBA theo trường hợp cạnh - cạnh - cạnh hoặc cạnh - góc - cạnh
a) widehat{ADC}widehat{DAB}
b) widehat{ACD}widehat{DBA}
c) widehat{CAD}widehat{BDA}
d) CDBA
Đọc tiếp
Cho hình bs.2

Trong các khẳng định sau, khẳng định nào đúng ? khẳng định nào sai ?
Bổ sung thêm điều kiện sau thì \(\Delta ACD=\Delta DBA\) theo trường hợp cạnh - cạnh - cạnh hoặc cạnh - góc - cạnh
a) \(\widehat{ADC}=\widehat{DAB}\)
b) \(\widehat{ACD}=\widehat{DBA}\)
c) \(\widehat{CAD}=\widehat{BDA}\)
d) \(CD=BA\)
Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt cạnh AC tại D. Trên cạnh BC lấy điểm E sao cho BE=BA
a) Chứng minh ∆ABD=∆EBD
b) Tính số đo góc BED
c) Trên tia đối của tia AB lấy điểm F sao cho AF=EC. Chứng minh: E,D,F thẳng hàng
d) C...
Xem chi tiết
Cho góc xOy khác góc bẹt . Trên cạnh Ox lấy các điểm A,B (OA nhỏ hơn OB ) trên cạnh Oy lấy các điểm C,D sao cho OC=OA,OD=OB. Chứng minh rằng :
a) AD=BC
Lm hộ mik ![]() với !
với !
Trên hình 90 :
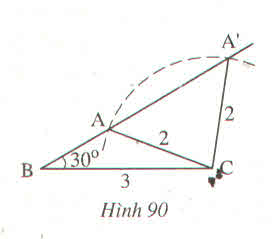
Các tam giác ABC và A'BC có cạnh chung BC = 3cm, CA = CA' = 2cm, \(\widehat{ABC}=\widehat{A'BC}=30^0\) nhưng hai tam giác đó không bằng nhau.
Tại sao ở đây không thể áp dụng trường hợp cạnh - góc - cạnh để kết luận \(\Delta ABC=\Delta A'BC\) ?
CHO DEF VUÔNG TẠI D . TRÊN CẠNH EF LẤY K SAO CHO EK=ED . TIA PHÂN GIÁC CỦA GÓC E CẮT DF TẠI H
a) CHỨNG MINH DH=HK
b) TÍNH GÓC EKH
Cho tam giác ABC vuông tại A . Trên cạnh BC lấy điêm E sao cho BE=BA . Tia phân giác của góc B cắt AC ở D
a) Chứng minh tám giác ABD=tam giác EBD
b) Chứng minh DE vuông góc với BC
c) Trên tia đối của tia AB lấy điểm F sao cho AF =EC . Chứng minh DC=DF và ba điểm E,D,F thẳng hàng







