Bài 6: Diện tích đa giác
Các câu hỏi tương tự
Cho hình chữ nhật ABCD. Từ A và C kẻ AE và CF vuông góc với BD tại E và F.
a) Chứng minh 2 đa giác ABCFE và ADCFE có diện tích bằng nhau
b) Tính diện tích của hai đa giác nói trên nếu các cạnh của hơn tỉ lệ với 4 và 3. Chu vi của hơn là 56cm.
Tính diện tích của hình được cho trong mỗi trường hợp sau đây :
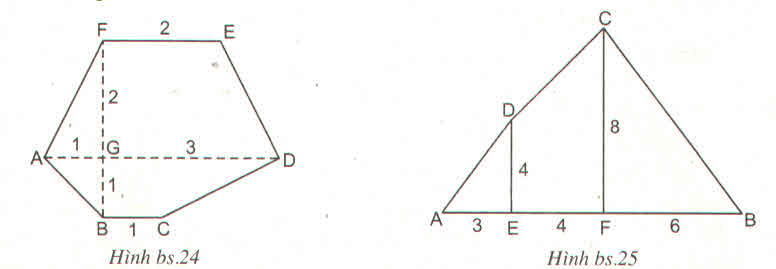
a) Đa giác ABCDEF, biết AD = 4cm, BC = 1cm, FE = 2cm, FB = 3cm, FB vuông góc với AD như hình bs.24
b) Cho đa giác ABCD, CF và DE đều vuông góc với AB (như hình bs.25)
Biết AB = 13 cm, CF = 8cm, DE = 4cm, FB = 6cm và AE = 3cm. Tính diện tích đa giác ABCD
Cho tam giác ABC vuông tại A, AF = 1,62cm; HC = 2,5cm, GC = 2cm, BD = 1,5cm;
BA = 3,7 cm. Biết tam giác BDE đều, HG vuông góc với GC, tính diện tích đa giác DEGHF.
Cho hình bình hành ABCD, với diện tích S và AB = a, AD = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính thep a, b cad S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là cạnh của hình bình hành đã cho ?
Tính diện tích của một tam giác cân có cạnh đáy là a, cạnh bên bằng b. Từ đó hãy tính diện tích của một tam giác đều có cạnh bằng a.
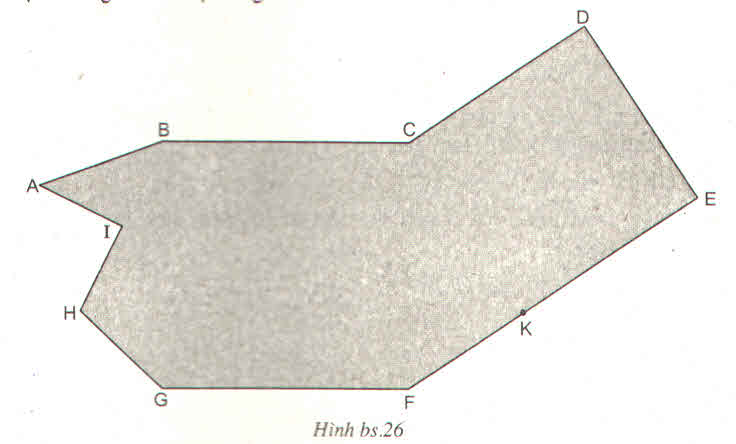
Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs.26
Tính diện tích của đa giác đó, biết rằng : KH song song với BC (K thuộc EF); BC song song với GF; CF song song với BG; BG vuông góc với GF; CK song song với DE; CD song song với FE; KE DE và KE vuông góc với DE; I là trung điểm của BH; AI IH và AI vuông góc với IH; HK 11 cm; CF 6cm. HK cắt CF tại J và JK 3cm, JF 2cm. BG cắt HK tại M và HM 2cm
Đọc tiếp
Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs.26
Tính diện tích của đa giác đó, biết rằng : KH song song với BC (K thuộc EF); BC song song với GF; CF song song với BG; BG vuông góc với GF; CK song song với DE; CD song song với FE; KE = DE và KE vuông góc với DE; I là trung điểm của BH; AI = IH và AI vuông góc với IH; HK = 11 cm; CF = 6cm. HK cắt CF tại J và JK = 3cm, JF = 2cm. BG cắt HK tại M và HM = 2cm
cho hbh ABCD với diện tích và AB=a,BC=b.Lấy mỗi cạnh của hbh đó làm cạnh dựng 1 hình vuông ra phía ngoài hbh .Tính theo a,b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là canh của hbh đã cho.






